Changing colors and scale in a Contour Plot

Question

I am struggling with a very basic functionality of Mathematica. I have the following code:

 Table[ContourPlot[![\[][1]][1]
  CentralizationBenefitSharingGraph[cM, cR, cS], {cM, 0, 1}, {cR, 0, 
   1}, FrameLabel -> Automatic, PlotLegends -> Automatic, 
  PlotPoints -> 100, 
  PlotLabel -> Row[{"cS = ", Round[cS, .01]}]], {cS, 0, 1, 1/10}]

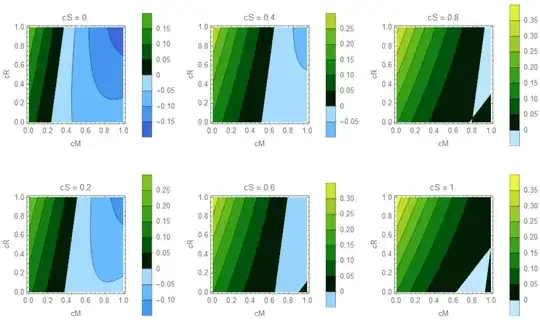
Which results in a series of plots in this fashion:

Now I would like to have the values above 0 to become an increasingly intenser green and those below zero an increasingly intenser red. Towards 0 I'd like to see a sort of 'fade' for my colors.

Also, is there some way to increase the scale such that I see more and the same amount of value ranges throughout my different plots?

Thank you folks kindly in advance for your help!

EDIT:

So I've been playing around with the options and got close to what I actually intend to achieve.

I have the following functions now:

For explaining the colorscheme:

scheme = (Blend[{Red, Yellow, Green}, Rescale[#1, {-0.3, 0.3}]] &);

BarLegend[{scheme[#] &, {-0.30, 0.3}}]

My actual plot:

Table[CountourPlot[
  CentralizationBenefitSharingGraph[cM, cR, cS], {cM, 0, 1}, {cR, 0, 
   1}, ColorFunction -> scheme, ColorFunctionScaling -> False, 
  FrameLabel -> Automatic, PlotLegends -> Automatic, 
  PlotPoints -> 1000, 
  PlotLabel -> Row[{"cS = ", Round[cS, .01]}]], {cS, 0, 1, 1/5}]

My underlying function:

 CentralizationBenefitGraph[cM,cS,cR]=0.314728 (2.907 + 0.806994 cM^2 + (-1.91571 + 0.806994 cS) cS + 
          cM (-1.11364 - 0.500185 cS - 0.147994 (1 + 1.566 cS))) - 
       0.15612 (5.35936 + 0.806994 cR^2 - 4.44322 cS + 1.45823 cS^2 + 
          cR (-1.11364 - 0.500185 cS - 0.147994 (1 + 1.566 cS)))

This results in the following kind of plots:

Two things left I'd like to achieve:

1. Having my Bar Legend fixed from 0.3 to -0.3 and in steps of e.g. 0.05.
2. Having my colorscheme range from 0.3, being intense green, to 0, being a faded green. And the other way from 0 to 0.3 in an increasingly intense red. So basically, everything > 0 is going to be increasingly green, everything < 0 increasingly red.

Any help is again much appreciated!

Answer 1

Try with the option:

ColorFunction -> ColorData[{"WatermelonColors", "Reverse"}]

In your code:

Table[ContourPlot[![\[][1]][CentralizationBenefitSharingGraph[cM, cR, cS], {cM, 0, 1}, {cR, 0, 1}, FrameLabel -> Automatic, 
PlotLegends -> Automatic, 
ColorFunction -> ColorData[{"WatermelonColors", "Reverse"}],      
PlotPoints -> 100, 
PlotLabel -> Row[{"cS = ", Round[cS, .01]}]], {cS, 0, 1, 1/10}]

(next time pls provide the function as well so that we can plot it for testing)

For more color schemes see MMA guide - ColorSchemes

For custom color schemes see my answer here: Beautiful Temperature Map

For the plot ranges, see link above and also this: PlotRange in DensityPlot

EDIT:

in response to your edit to the OP, you can try this:

scheme = (Blend[{RGBColor[0.74, 0, 0], RGBColor[0.75, 0.76, 0], 
      RGBColor[0, 0.64, 0]}, Rescale[#1, {-0.3, 0.3}]] &);
BarLegend[{scheme[#] &, {-0.30, 0.3}}, 6]


Table[ContourPlot[
  CentralizationBenefitGraph[cM, cR, cS], {cM, 0, 1}, {cR, 0, 1}, 
  ColorFunction -> scheme,
  ColorFunctionScaling -> False,
  FrameLabel -> Automatic,
  PlotLegends -> BarLegend[{scheme[#] &, {-0.3, 0.3}}, 7],
  PlotPoints -> 100,
  PlotRange -> All,
  PlotLabel -> Row[{"cS = ", Round[cS, .01]}]]
 , {cS, 0, 1, 1/5}]

Answer 2

Edit

     colorWig[z_] := 
 Which[-0.4 < z <= 0, 
  ColorData["DeepSeaColors"][Rescale[z, {-0.4, 0}]], 0 <= z < 0.4, 
  ColorData["AvocadoColors"][Rescale[z, {0, 0.4}]]]

centralizationBenefitGraph[cM_, cS_, cR_] := 
 0.314728 (2.907 + 0.806994 cM^2 + (-1.91571 + 0.806994 cS) cS + 
     cM (-1.11364 - 0.500185 cS - 0.147994 (1 + 1.566 cS))) - 
  0.15612 (5.35936 + 0.806994 cR^2 - 4.44322 cS + 1.45823 cS^2 + 
     cR (-1.11364 - 0.500185 cS - 0.147994 (1 + 1.566 cS)))

Multicolumn@
 Table[ContourPlot[
   centralizationBenefitGraph[cM, cR, cS], {cM, 0, 1}, {cR, 0, 1}, 
   ColorFunction -> colorWig, ColorFunctionScaling -> False, 
   FrameLabel -> Automatic, 
   PlotLegends -> 
    BarLegend[{colorWig@# &, {-0.4, 0.4}}, 
     Ticks -> Range[-0.4, 0.4, 0.05]], PlotPoints -> 100, 
   PlotLabel -> Row[{"cS = ", Round[cS, .01]}]], {cS, 0, 1, 1/5}]

colorWig[z_] := 
     Which[-0.4 < z <= 0, 
      ColorData["DeepSeaColors"][Rescale[z, {-0.4, 0}]], 0 <= z < 0.4, 
      ColorData["AvocadoColors"][Rescale[z, {0, 0.4}]]]

    centralizationBenefitGraph[cM_, cS_, cR_] := 
     0.314728 (2.907 + 0.806994 cM^2 + (-1.91571 + 0.806994 cS) cS + 
         cM (-1.11364 - 0.500185 cS - 0.147994 (1 + 1.566 cS))) - 
      0.15612 (5.35936 + 0.806994 cR^2 - 4.44322 cS + 1.45823 cS^2 + 
         cR (-1.11364 - 0.500185 cS - 0.147994 (1 + 1.566 cS)))

    Multicolumn@
     Table[ContourPlot[
       centralizationBenefitGraph[cM, cR, cS], {cM, 0, 1}, {cR, 0, 1}, 
       ColorFunction -> colorWig, ColorFunctionScaling -> False, 
       FrameLabel -> Automatic, PlotLegends -> Automatic, 
       PlotPoints -> 100, 
       PlotLabel -> Row[{"cS = ", Round[cS, .01]}]], {cS, 0, 1, 1/5}]