Efficient way to detect peak value changes in a list

Question

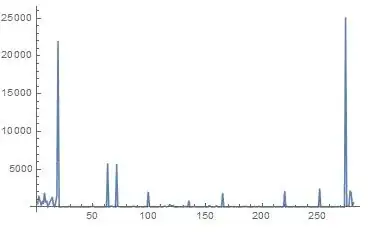
ListPlot[list, Joined -> True, PlotRange -> Full]

I would like a simple method to get the positions within the list where the values deviate a lot from their previous values. If I just use a threshold, I might miss some peaks or introduce wrong results as the values before a peak can vary.

Here is the list:

list = Import["https://pastebin.com/raw/ncJDt0L4", "List"]

I was thinking of using a numeric gradient, but I don't know if Mathematica has a build in function and also if this is really the best method.

EDIT:

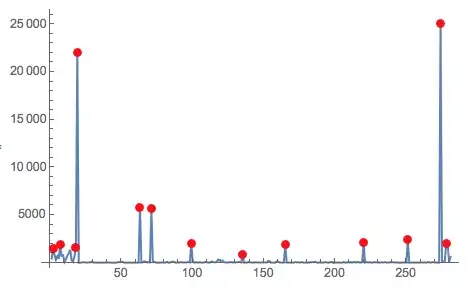
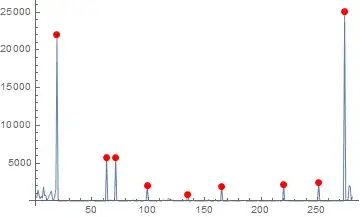
I forgot to mention: A peak should always be chosen with respect to the previous points which lie after the last detected peak, or in other terms: All values before the last detected peak should not be considered in evaluating the next peak. Only the values after the last detected peak are of importance.

The first small peaks before the first big peak should not be detexted as peaks since the data fluctuates a lot there

...and the last little peak should not be counted as peaks, because there cannot be two peaks when the distance (x) between the peak position is less than 3.

@DavidG.Stork Interesting, thanks for the note. How would you use it in this case? — james, Aug 14 '18 at 18:30
ListConvlve the data with a "center-surround" filter that will "pick out" peaks. — David G. Stork, Aug 14 '18 at 23:02

score 5 · Answer 1 · edited Jun 16 '20 at 09:23

5

Using FindPeaks is a fine solution. This answer responds to the following OP statements/questions.

I would like a simple method to get the positions within the list where the values deviate a lot from their previous values. If I just use a threshold, I might miss some peaks or introduce wrong results as the values before a peak can vary.

I was thinking of using a numeric gradient, but I don't know if Mathematica has a build in function

Get the (consecutive) differences:

ds = Differences[list];
Through[{Min, Max, Mean, Median, StandardDeviation}[ds]]
(* {-24958.8, 25131.1, 0.526443, -1.1353, 2896.09} *)

Pick peak positions with a threshold (0.06 here):

ds2 = Select[ds, # > 0 &];
pos = Pick[Range[2, Length[list]], 
  Map[ # > Mean[ds2] + 0.06*StandardDeviation[ds2] &, ds]]

Plot data and peaks:

list2 = Transpose[{Range[Length[list]], list}];
ListLinePlot[list2, PlotRange -> Full, 
 Epilog -> {Red, PointSize[Large], Point[list2[[pos]]]}]

edited Jun 16 '20 at 09:23

Community

1

answered Aug 14 '18 at 19:44

Anton Antonov

37,787
3
100
178

Thanks a lot for your answer. Do you see a method of how to avoid those initial peaks, because they should theoretically not be seen as peaks. – james Aug 14 '18 at 20:05
see Edited question – james Aug 14 '18 at 20:13
@james I thought the initial peaks are important! ;) And yes there is a method to avoid them... – Anton Antonov Aug 14 '18 at 20:19
okay, awesome. Looking forward seeing it. – james Aug 14 '18 at 20:25
which method is it that you were thinking of ? – james Aug 15 '18 at 08:55
@james Quantile Regression. See this MSE post : https://mathematica.stackexchange.com/a/125001/34008 . – Anton Antonov Aug 15 '18 at 09:06
Thank you for the link. I am having difficulties understanding the method. If you have the time and if it is not too much asked, do you think that you could add the solution to your answer ? – james Aug 15 '18 at 10:40
@james I will post another answer later today. – Anton Antonov Aug 15 '18 at 13:36
Thanks so much ! – james Aug 15 '18 at 14:55
@james I did experiment with Quantile regression on this but the results are not much better... – Anton Antonov Aug 16 '18 at 08:37
Okay, well thanks a lot for trying! – james Aug 17 '18 at 10:35

Johu · Accepted Answer · 2018-08-18T11:48:08.447

FindPeaks is the perfect solution as it has all the options to fine tune the condition you require for a peak:

list = Import["https://pastebin.com/raw/ncJDt0L4", "List"];

peaks = FindPeaks[list, 3, 12];
ListLogPlot[{list, peaks}, PlotRange -> Full, Joined -> {True, False},
  PlotStyle -> {Thin, Directive[Red, PointSize[Large]]}]

Just play around with the values for Gaussain blurring, minimum sharpness and threshold until you get the performance you want.

Edit

The log-plot is very useful for highlighting the reason, why the smallest peaks are also considered a peak. In case you do not consider it a peak, you can easily eliminate the very small but sharp features by also using the threshold, the fourth argument of FindPeaks.

For a direct comparison with other solutions, here is a linear plot:

ListPlot[{list, peaks}, PlotRange -> Full, Joined -> {True, False}, 
 PlotStyle -> {Thin, Directive[Red, PointSize[Large]]}]

Thanks a lot ! The Log plot is great, but can you also add a linear plot for direct comparaison with the other answers? — james, Aug 18 '18 at 02:00

score 4 · Answer 3 · answered Aug 14 '18 at 19:03

4

I think that you are likely looking for some combination of the parameters of the FindPeak function, for example:

list = Import["https://pastebin.com/raw/ncJDt0L4", "List"];

peaks = FindPeaks[list, Automatic, Automatic, 500];
ListLinePlot[
 list,
 PlotRange -> Full,
 Epilog -> {Red, PointSize[Large], Point[peaks]}
 ]

Mathematica graphics

answered Aug 14 '18 at 19:03

C. E.

70,533
6
140
264

Thanks a lot for your answer. Do you see a method of how to avoid those initial peaks, because they should theoretically not be seen as peaks. – james Aug 14 '18 at 20:05
@james Why shouldn't they be seen as peaks? – C. E. Aug 14 '18 at 20:06
The values before the first peak fluctuate and hence should not be seen as peaks, but rather as noise with respect to the first peak. I forgot to mention: The peaks should always be chosen with respect to the previous points which lie after the last peak. – james Aug 14 '18 at 20:10
@james Is there a specific minimum separation between peaks before they are seen as separate peaks, rather than part of some larger peak? – C. E. Aug 14 '18 at 20:13
Hmm, good question. Yes, in principle, the minimum separation would probably be 3. – james Aug 14 '18 at 20:20
FindPeaks is exactly for this purpose. It has extra options to set required derivetives and contrasts to be considered a peak. Have you not noticed these options or are they not suitable for you? – Johu Aug 17 '18 at 14:44

Efficient way to detect peak value changes in a list

3 Answers3