FunctionTreeForm

Question

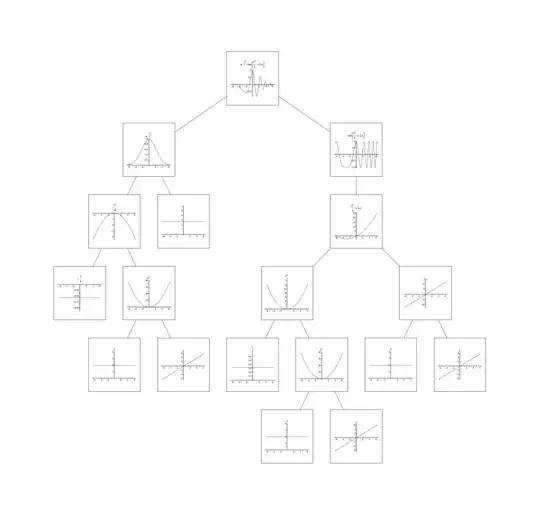
I'd like to implement a function FunctionTreeForm which takes an arbitrary complex function and renders all the captionable subfunctions in a TreeForm.

• Explanation

If we take e.g. a function:

TreeForm[Exp[-(x/3)^2]*Cos[2 x + x^2/3]]

the corresponding TreeForm is:

If we tokenize this function into its subfunctions and plot them seperately:

{Plot[Exp[-(x/3)^2]*Cos[2 x + x^2/3], {x, -2 \[Pi], 2 \[Pi]}, 
PlotLegends -> "Expressions"], 
Plot[E^(-(x^2/9)), {x, -2 \[Pi], 2 \[Pi]}, PlotLegends -> "Expressions"],
Plot[Cos[2 x + x^2/3], {x, -2 \[Pi], 2 \[Pi]}, PlotLegends -> "Expressions"],
Plot[2 x + x^2/3, {x, -2 \[Pi], 2 \[Pi]}, PlotLegends -> "Expressions"]}

we get:

What I'd like to do is to traverse the corresponding TreeForm and check if a Node is not an Atomic. If it is not I'd suspect it is a function. After collecting all these plots I'd like to display the corresponding TreeForm as a plot of the main function and all its sub-functions in TreeForm.

I played around with Level[] etc. but did not came to a solution that does reliable tokenisation of a function definition into sub-functions and I totally lack any idea how to transfer these into a Tree representation.

• Why I think this could be a feasible functionality

I think in education this FunctionTreeFrom could give a good clue how a rather complicated function is actually assembled from its sub-functions.

I hope this is an interesting question and I'm eager to learn how to tackle problems like that.

Answer 1

Here's an approach - I hope this is what you are looking for. What I did: With cases I just take the nodes that are not Atoms on every level and plot just as you did. Additionally, I included the trees

tf = TreeForm[Exp[-(x/3)^2]*Cos[2 x + x^2/3]];

Grid[{Plot[#, {x, -2 \[Pi], 2 \[Pi]}, PlotLegends -> "Expressions"], 
TreeForm[#, ImageSize -> Small]} & /@ 
Reverse[Cases[tf, x_ /; AtomQ[x] == False, Infinity]]]

Alternatively, you could exclude nodes, something like

Grid[{Plot[#, {x, -2 \[Pi], 2 \[Pi]}, PlotLegends -> "Expressions"], 
TreeForm[#, ImageSize -> Small]} & /@ 
Reverse[Cases[tf, x : Except[_Integer | _Symbol | _Rational], Infinity]]]

(this could be helpful if you wanted to exclude Power or Times)

(Edit: I added Reverse, to go Top-Down)

EDIT 2 - Plot in "TreeForm" As discussed, I tried to implement the idea that the plots are in actual tree for, i.e. in the respective vertices. Here's how I tried to do it - I am sure there are better ways... Please note that I didn't thoroughly test the function, so any feedback is welcome.

TODO: One problem I couldn't solve is the ImageSize. I did link it to LeafCount, but sometimes you want to add some pixels or make it smaller. For now, you can use the 4th argument of the function to adjust. Any ideas welcome!

So the function:

ClearAll[functionTree];
functionTree[function_, plotMin_, plotMax_, imSizeCorrection_, 
correction_: 0.3] := Module[{tree, nodes, pos, rules},
   tree = TreeForm[function];
   nodes = Union[Cases[tree, x_ :> {x, Position[tree, x]}, Infinity]];
   pos = Flatten[nodes[[All, 2]], 1];
   rules = 
     Flatten[Position[pos, #][[1, 1]] -> 
     Position[pos, Most[#]][[1, 1]] & /@ Cases[pos, Except[{1}]]];
   TreePlot[rules, Automatic, Position[pos, {1}][[1, 1]], 
     ImageSize -> LeafCount[function]*100 + imSizeCorrection, 
     VertexRenderingFunction -> ({White, EdgeForm[Black], 
     Rectangle[#1 - correction, #1 + correction], Black, 
     Text[Plot[
     nodes[[Position[nodes, pos[[#2]], Infinity][[1, 1]], 1]], {x,
       plotMin, plotMax}, 
     PlotLabel -> 
      nodes[[Position[nodes, pos[[#2]], Infinity][[1, 1]], 
        1]]], #1]} &)]
]

e.g. function call:

functionTree[Exp[-(x/3)^2]*Cos[2 x + x^2/3], -2 \[Pi], 2 \[Pi], 0, 0.3]

What it does: first we collect all nodes, killing duplicates. In pos we keep all positions, i.e. all nodes in the tree. Next, rules generates the edges of the tree (i.e. it finds the respective roots, except for the top node). Next we can plot it all - with above discussed problem (ImageSize that is). We use VertexRenderingFunction to get it done.

Note that nodes and pos in this construction do not necessarily have the same Length, for there can be several nodes with the same content (such as x).

Also note: I figured I might just as well plot all nodes - why exculde the non-atomic ones after all? - else see the first answer.

I hope this helps - feedback very welcome, especially on the ImageSize thingie.

(first img removed)