How to solve 2D PDE with a constraint?

Question

As related to the 2D+1 PDE problem,

if now I would like to solve the stationary solution which satisfies $\partial_t u(t,x,y)=0$.

Or equivalently,

$-y\partial_{x}u+\partial_{y}\left[a y+b sin(x)u+c\partial_{y}u\right]=0$

ωcb = -50;
ωct = 50;
ωb = -5;
ωt = 5;
A = 10;
γ = 0.1;
kT = 0.1;


With[{u = u[θ, ω]}, 
  eq = -D[ω u, θ] - D[-A Sin[θ] u, ω] - γ kT D[u, ω] + γ  D[ω u, ω]==0
];

ufun = NDSolveValue[{eq, u[-π, ω] == u[π, ω], u[θ, ωcb] == u[θ, ωct]},u, {θ, -π, π}, {ω, ωcb, ωct}]; 


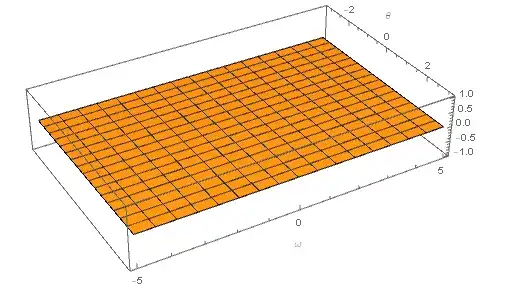
Plot3D[Abs[ufun[θ, ω]], {θ, -π, π}, {ω, ωb, ωt}, 
PlotRange -> All, AxesLabel -> Automatic, PlotPoints -> 50, 
BoxRatios -> {Pi, ωb, 1}]

We see the message:

NDSolveValue::femibcnd: No DirichletCondition or Robin-type NeumannValue was specified for {u}; the result may not be unique.
NDSolveValue::femcscd: The PDE is convection dominated and the result may not be stable. Adding artificial diffusion may help.

As expected, the solution is not unique.

Since the function $u(x,y)$ represents the probability density function, namely, we have the normalization condition :$\int dx\int dy \text{ }u(x,y)=1$.

Question: Is it possible to include this additional constraint in NDSolve to make it unique?

Note:

For the boundary condition, we have $u(-\pi,y)=u(\pi,y)$. In $y$-direction, it is unbounded, but in the code I use a periodic boundary condition at some cutoff coordinates to mimic the case without boundary.

Answer 1

Here we have an equation of parabolic type whose solution is defined in two squares $xy>0$. In two other squares where $xy<0$ the solution diverges under any conditions. To determine the solution, we must specify initial conditions for $x = 0$ and boundary conditions.

{a, b, c, k, L, y0, T} = {1, 10, 1, 1, 5, 10^-3, Pi};
u0[y_] := Exp[-(y^2)/2]/(2*Pi)
eq = k*y*D[u[x, y], x] - 
   D[a*y + b*Sin[x]*u[x, y] + c*D[u[x, y], y], y];
ic = u[0, y] == u0[y];
bc = {u[x, y0] == u0[y0], u[x, L] == u0[L]};
sol = NDSolveValue[{eq == 0, ic, bc}, u, {x, 0, T}, {y, y0, L}]
Plot3D[Abs[sol[x, y]], {x, 0, Pi}, {y, y0, L}, PlotRange -> All, 
 ColorFunction -> "LakeColors", Mesh -> None]

Example of a solution with symmetric boundary conditions on the edges

{a, b, c, k, L, y0, T} = {1, 10, 1, 1, 5, 10^-3, 4*Pi};
u0[y_] := Exp[-(y - L/2)^2/2]/(2*Pi)
eq = k*y*D[u[x, y], x] - 
   D[a*y + b*Sin[x]*u[x, y] + c*D[u[x, y], y], y];
ic = u[0, y] == u0[y];
bc = {u[x, y0] == u0[y0], u[x, L] == u0[L]};
sol = NDSolveValue[{eq == 0, ic, bc}, u, {x, 0, T}, {y, y0, L}]
Plot3D[Abs[sol[x, y]], {x, 0, T}, {y, y0, L}, PlotRange -> All, 
 ColorFunction -> "LakeColors", Mesh -> None, AxesLabel -> Automatic, 
 PlotPoints -> 50]