I'm newbie here, and using Mathematica for two weeks, so, anyone can help me with this? I tried using the Findroot command but I don't get it. Thanks in advance guys.
Asked
Active
Viewed 272 times
0
-
Possible duplicate: https://mathematica.stackexchange.com/questions/176257/finding-root-of-besselj – Michael E2 Aug 20 '18 at 00:02
2 Answers
5
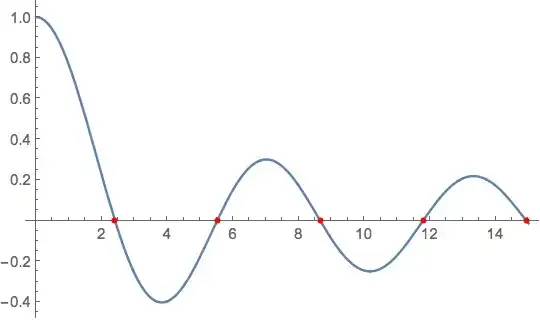
f[x_] := BesselJ[0, x]
Plot[f[x], {x, 0, 15},
Epilog -> {Red, AbsolutePointSize[4],
Tooltip[Point[{BesselJZero[0, #], 0}], BesselJZero[0, #] // N] & /@
Range[5]}]
To see the progressive estimates using Newton-Raphson, use FixedPointList
(sol1a = Table[
FixedPointList[# - f[#]/f'[#] &, x0], {x0, 3., 15, 3}]) // Column
To see just the final values use FixedPoint
(sol1b = Table[FixedPoint[# - f[#]/f'[#] &, x0], {x0, 3., 15, 3}])
(* {2.40483, 5.52008, 8.65373, 11.7915, 14.9309} *)
Alternatively, using NestList or Nest
(sol2a = Table[
NestList[# - f[#]/f'[#] &, x0, 10], {x0, 3., 15., 3.}]) // Column
(sol2b = Table[Nest[# - f[#]/f'[#] &, x0, 10], {x0, 3., 15., 3.}])
(* {2.40483, 5.52008, 8.65373, 11.7915, 14.9309} *)
Using FindRoot
sol3 = x /. FindRoot[BesselJ[0, x] == 0, {x, #}] & /@ Range[3., 15, 3]
(* {2.40483, 5.52008, 8.65373, 11.7915, 14.9309} *)
Using NSolve
sol4 = x /. NSolve[{BesselJ[0, x] == 0, 0 < x < 15}, x]
(* {2.40483, 5.52008, 8.65373, 11.7915, 14.9309} *)
Solve or Reduce give the solution in terms of BesselJZero
x /. Solve[{BesselJ[0, x] == 0, 0 < x < 15}, x]
(* {BesselJZero[0, 1], BesselJZero[0, 2], BesselJZero[0, 3], BesselJZero[0, 4],
BesselJZero[0, 5]} *)
x /. {ToRules[Reduce[{BesselJ[0, x] == 0, 0 < x < 15}, x]]}
(* {BesselJZero[0, 1], BesselJZero[0, 2], BesselJZero[0, 3], BesselJZero[0, 4],
BesselJZero[0, 5]} *)
Comparing with the BesselJZero values
bjz = BesselJZero[0, #] & /@ Range[5];
sol1a[[All, -1]] == sol1b == sol2a[[All, -1]] == sol2b == sol3 == sol4 == bjz
(* True *)
Bob Hanlon
- 157,611
- 7
- 77
- 198
-
thanks for the answer, but I do not have a formula, that's what I do not understand, how do I apply it? – shatman Aug 20 '18 at 13:10
-
You gave Newton-Raphson formula, i.e.,
x[i+1] == x[i] - f[x[i]]/f'[x[i]]. When written as apure functionthe RHS is# - f[#]/f'[#] &.FixedPointListandFixedPointiterate this pure function until the results converge and stops automatically.NestListandNestiterates the pure function a specified number of times. For a sufficiently large number of specified iterations the result will converge to the fixed point. In all of these cases a starting value (x[0]) must be specified that is in the region of the desired root. – Bob Hanlon Aug 20 '18 at 14:35 -
0
f[x_] := BesselJ[0, x]
x[0] = 1.;(*initial point*)(*different initial point converge to different root*)
Table[x[i + 1] = x[i] - f[x[i]]/f'[x[i]]; x[i], {i, 0, 10}]
{1., 2.73889, 2.36779, 2.40456, 2.40483, 2.40483, 2.40483, 2.40483,2.40483, 2.40483, 2.40483}
x[0] = 5.;(*initial point*)
Table[x[i + 1] = x[i] - f[x[i]]/f'[x[i]]; x[i], {i, 0, 10}]
{5., 5.54215, 5.52003, 5.52008, 5.52008, 5.52008, 5.52008, 5.52008, 5.52008, 5.52008, 5.52008}
OkkesDulgerci
- 10,716
- 1
- 19
- 38