How to use Mathematica to plot an ellipse given foci and semimajor axis?

Question

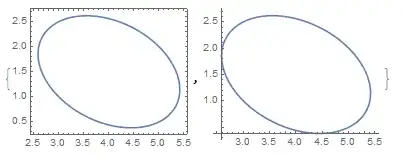
How can I use Mathematica (version 9) to plot an ellipse, given the coordinates of its two foci and the length of its semimajor axis, where the major axis is not necessarily parallel to either the $x$-axis or the $y$-axis? I also need the scales of the two axes to be equal.

For example, the foci might be at $(3,2)$ and $(5,1)$ and the semimajor axis might be $1.7$.

The following gives an ellipse of the right size, shape, and centre, but wrong orientation:

Graphics[Circle[{4, 1.5}, {1.7, Sqrt[1.64]}]]

Is this a Mathematica question ? How would you do it outside Mathematica ? — Lotus, Aug 27 '18 at 13:00
Welcome to Mathematica.SE. Are you sure you are posting on the right site? There is nothing in your question making it clear that it is concerned with Mathematica software. — m_goldberg, Aug 27 '18 at 14:13

score 3 · Accepted Answer · edited Mar 08 '19 at 11:58

You can find a geometric solution to this problem by using an implicit region definition directly based on the definition of an ellipse: sum of distances from foci equals twice the semimajor axis.

With[{foci = {{3, 2}, {5, 1}}, semimajoraxis = 3/2},
 Region[ImplicitRegion[
   Sum[EuclideanDistance[{x, y}, p], {p, foci}] == 
    2 semimajoraxis, {x, y}],
  Axes -> True, Epilog -> {Red, Point[foci]}]]

Geometric regions functionality was introduced in Mathematica 10. Similar things can be accomplished using RegionPlot on earlier versions, but it requires explicit plot range, which complicates the approach (basically here I define the plot range to be $\pm \mathtt{semimajoraxis}$ on $x$ and $y$ axes).

With[{foci = {{3, 2}, {5, 1}}, semimajoraxis = 3/2},
 RegionPlot[
  Sum[EuclideanDistance[{x, y}, p], {p, foci}] < 2 semimajoraxis, 
  Evaluate[Sequence @@ 
    MapThread[{#1, #2 - semimajoraxis, #2 + semimajoraxis} &, {{x, y},
       Mean[foci]}]],
  AspectRatio -> Automatic, PlotStyle -> None, 
  Epilog -> {Red, Point[foci]}]]

I hope this works for you, since my v9 seems to nag about need for legacy Java. Does it work?

Many thanks for this. It's just what I need, but can it be made to work for Mma v9? — , Aug 27 '18 at 15:29
@ruffle Oh my. Geometric regions functionality was introduced in v10. I'll add a RegionPlot variant which should work in v9 in a moment. — kirma, Aug 27 '18 at 15:34

matrix42 · Answer 2 · 2018-08-28T03:52:00.417

foci = {{3, 2}, {5, 1}};
a = 3/2;

{{x1, y1}, {x2, y2}} = foci;
d = EuclideanDistance @@ foci;

{ContourPlot[Sum[EuclideanDistance[{x, y}, p], {p, foci}] == 2 a, 
{x, 2.5, 5.5}, {y, 0.3, 2.7}, AspectRatio -> Automatic], 

 ParametricPlot[{(x1 + x2)/2, (y1 + y2)/2} + 
  {a/d (x2 - x1) Cos[t] + Sqrt[a^2/d^2 - 1/4] (y1 - y2) Sin[t], 
   a/d (y2 - y1) Cos[t] + Sqrt[a^2/d^2 - 1/4] (x2 - x1) Sin[t]}, 
   {t, 0, 2 Pi}]
}

score 3 · Answer 3 · answered Feb 24 '19 at 00:24

I came across this (not so recent) question, and it occurs to me that the following code is simpler - assuming all you want is the plot:

foci = {{3, 2}, {5, 1}}; semimajoraxis = 3/2; 
Graphics[{Rotate[Circle[Mean[foci], {3/2, 1}], 
   VectorAngle[{1, 0}, foci[[1]] - Mean[foci]]], 
   {Red, 
   Point /@ {foci, Mean[foci]}}}, Axes -> True, 
   AxesOrigin -> {2.5, 0}]

Tomas Garza

score 2 · Answer 4 · answered Feb 24 '19 at 02:19

I will note that one can use Ellipsoid[] for this:

With[{f1 = {3, 2}, f2 = {5, 1}, a = 17/10},
     With[{r = RotationMatrix[{{1, 0}, f2 - f1}]},
          Graphics[{Directive[EdgeForm[ColorData[97, 1]], FaceForm[]], 
                    Ellipsoid[(f1 + f2)/2, 
                              r.DiagonalMatrix[{a^2, a^2 - Norm[f1 - f2]^2/4}].Transpose[r]]},
                   Frame -> True]]]

ellipse

If one is dissatisfied with Ellipsoid[] (like in this answer), one could also fall back on the NURBS representation. Here is a routine for making the BSplineCurve[] equivalent of Ellipsoid[]:

makeEllipse[p_?VectorQ, m_?MatrixQ] := Module[{aff, eig},
    eig = Eigensystem[N[m]];
    aff = AffineTransform[{Transpose[eig[[2]]].DiagonalMatrix[Sqrt[eig[[1]]]], p}];
    BSplineCurve[aff[{{1, 0}, {1, 1}, {-1, 1}, {-1, 0}, {-1, -1}, {1, -1}, {1, 0}}],
                 SplineClosed -> True, SplineDegree -> 2, 
                 SplineKnots -> {0, 0, 0, 1/4, 1/2, 1/2, 3/4, 1, 1, 1}, 
                 SplineWeights -> {1, 1/2, 1/2, 1, 1/2, 1/2, 1}]]

and now one can use makeEllipse[] as a replacement for Ellipsoid[] in the code given above.

score 1 · Answer 5 · answered Nov 28 '19 at 00:41

1

You can use the "SplineCircle" resource function to specify the semimajor axis direction:

Graphics[
    {
    ResourceFunction["SplineCircle"][{4,1.4}, {1.7,Sqrt[1.64]}, {2,-1}],
    Red, Point[{{3,2}, {5,1}}]
    },
    Axes->True
]

answered Nov 28 '19 at 00:41

Carl Woll

130,679
6
243
355

How to use Mathematica to plot an ellipse given foci and semimajor axis?

5 Answers5

Linked