Automated searching for maximal 2D point configurations

Question

I have some black-box function that takes lists of 2D points, and I would like to find some practical methods of searching for collections of points that maximize it.

Motivation

I've come across the need to search for sets of points in the plane that satisfy/optimize constraints so many times, but have never adequately found workable strategies in Mathematica. To name a few of these times:

• When packing geometric entities in various ways
• Searching for graph embeddings with certain properties
• Various combinatorial optimization problems

Minimal Example

Kobon triangles (mentioned in comments), is a nice example of this type of problem: searching for arrangements of lines that make the most triangles. Jason B. provided a brute-force solution to this problem by converting the lines to a graph, which is great, but to illustrate my question let's look at it this way: consider the following function f that takes (flattened) lines as arguments

(* the ith line is `InfiniteLine[{{xi1, yi1}, {xi1, yi2}}] *)
f[x11, y11, x12, y12, x21, y21, x22, y22, ...] := ...

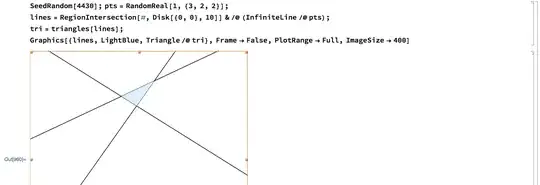
and returns the number of non-overlapping triangles. Here are some inputs pts where f is 1:

SeedRandom[4430];
pts = RandomReal[1, {3, 2, 2}];
lines = RegionIntersection[#, Disk[{0, 0}, 10]] & /@ (InfiniteLine /@ pts);
tri = triangles[lines];
Graphics[{lines, LightBlue, Triangle /@ tri}, Frame -> False, PlotRange -> Full]

Where I get stuck

I first tried using FindMaximum on the simplest case of only 3 lines (i.e. find 1 triangle from 12 coordinates). As you can see below, it fails to find a set of 6 points in the plane, even when supplied with the correct coordinates as starting values (which was very strange to me):

d = Disk[{0, 0}, 20];
s = FindMaximum[{f[x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, 
    y6], {x1, y1} \[Element] d && {x2, y2} \[Element] 
     d && {x3, y3} \[Element] d && {x4, y4} \[Element] 
     d && {x5, y5} \[Element] d && {x6, y6} \[Element] d}, 
    {{x1, 0.7242101930120808`}, {y1, 0.029677803428552307`}, {x2, 0.00816459598186059`}, {y2, 0.47699819634429996`}, {x3, 0.06540238199229464`}, {y3, 0.69214964488526`}, {x4,0.6253484480271967`}, {y4, 0.9545360094125843`}, {x5, 0.12098288193445206`}, {y5, 0.7013188710966709`}, {x6, 0.2806641729642241`}, {y6, 0.926496649677153`}}]

Neither NMaximize nor FindInstance seem up to the task either:

NMaximize[{f[x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, 
    y6], {x1, y1} \[Element] d && {x2, y2} \[Element] 
     d && {x3, y3} \[Element] d && {x4, y4} \[Element] 
     d && {x5, y5} \[Element] d && {x6, y6} \[Element] d}, {x1, y1, 
   x2, y2, x3, y3, x4, y4, x5, y5, x6, y6}, 
  Method -> "DifferentialEvolution"]

FindInstance[f[x1, y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6] == 1, {x1, y1, x2,
y2, x3, y3, x4, y4, x5, y5, x6, y6}, Reals, 1]

When the variables are continuous and the function you are looking to maximize is integer-valued, this is no doubt a hard problem. However, are there are definitely better ways out there to solve this than grid/random search?

Code for f in the above example

f[x1_, y1_, x2_, y2_, x3_, y3_, x4_, y4_, x5_, y5_, x6_, y6_] := 
 Module[{l, h, lines},
  l = InfiniteLine /@ {{{x1, y1}, {x2, y2}}, {{x3, y3}, {x4, 
       y4}}, {{x5, y5}, {x6, y6}} };
  lines = RegionIntersection[#, Disk[{0, 0}, 10]] & /@ l;
  Length[triangles@lines]
  ]

triangles[lines:{__}]:= Module[
    {lineSegments, vertices, edges, triangles},

    lineSegments = Flatten[
        Map[Function @ Partition[Sort @ #, 2, 1],
            Table[With[{l=
                List @@@ Map[RegionIntersection[Part[lines, n], #]&, Delete[lines, n]]},
                Flatten[Select[l, Depth[#] >= 3&], 1]
                ],
                {n, Length @ lines}
            ]
        ],
        1
    ]; 

   vertices = Flatten[lineSegments, 1] // DeleteDuplicates;
   edges = lineSegments /. MapIndexed[#1 -> First@#2 &, vertices];
   triangles = FindCycle[Graph[#1 \[UndirectedEdge] #2 & @@@ edges], {3}, All];
   triangles = triangles[[All, All, 1]];
   vertices[[#,1]] & /@ triangles
]

Additional Details

• A valid assumption is that all the points are in some Disk[{0, 0}, n] or another fixed region.

• Since this is useful for finding geometric configurations subject to constraints - perhaps FindGeometricConjectures would be a better fit to try (when v12 comes out)?