The following code gets all vertices of all polygons (mesh cells) of VoronoiMesh[pts]:
SeedRandom[3];
pts = RandomReal[{-1, 1}, {25, 2}];
mesh = VoronoiMesh[pts];
vertices = MeshCoordinates[mesh];
Show[mesh, Graphics[{Black, Point[pts], Red, Point[vertices]}]]
This outputs:
My question
How can I get a list of vertices for each polygon and compute the area of each polygon using the Shoelace formula?
The output should be similar to:
So, by clicking on the polygon number, it should show its vertices and its size.
I found this tool-tip image in Finding the perimeter, area and number of sides of a Voronoi cell

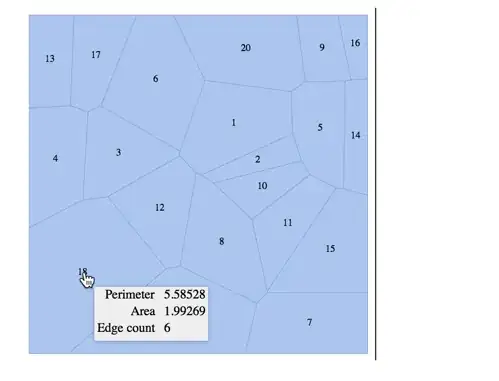

Areasuffice? – Greg Hurst Sep 08 '18 at 19:45shoelace formula, notbuilt-in function. – Eman Sep 08 '18 at 20:54