4

Given an arbitrary expression, how can I have Mathematica only evaluate the (bound) symbols, i.e. replace them by their respective values, but not do any further simplification/evaluation of the expression? Trace shows me that indeed the evaluation of the symbols is done first, but how to stop the standard evaluation procedure at this point?

Example:

a = 7
expr = d + a + 3

What I would like to obtain is d+7+3

I tried

HoldForm[expr] /. x_Symbol -> Evaluate[x]

but this gives the plain HoldForm of the expression. Symbol, by the way, is apparently not the Head of a bound symbol. In this case it is Integer. Apart from that, the replacement rule with the selected evaluation does not work at all. But I can't find anything better.

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
Roland Salz
  • 381
  • 1
  • 6
  • 1
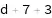
    Actually, a bound symbol has the head Symbol, but you must protect it from evaluation to see this. Try Head[Unevaluated[a]]. – John Doty Sep 09 '18 at 23:35

1 Answers1

3

Update: For the general case where you don't know which symbols have values you can use the methods from this answer by WReach and this by Leonid Shiffrin in combination with ValueQ:

a = 7; b = 5;
Defer[d + a + b + 3] /. s_Symbol :> RuleCondition[s, ValueQ[s]]
Defer[d + a + b + 3] /. s_Symbol /; ValueQ@s :> RuleCondition[s] 
Defer[d + a + b + 3] /. s_Symbol :> With[{e = s}, e /; ValueQ[s]] 
Defer[d + a + b + 3] /. s_Symbol /; ValueQ@s :> With[{e = s}, e /; True]

and the same expressions with HoldForm in place of Defer all give

d + 7 + 5 + 3

Original answer:

expr = With[{a = a}, Defer[d + a + 3]]

d + 7 + 3

Also

Defer[d + # + 3] & @ a 
With[{a = a}, HoldForm[d + a + 3]]
HoldForm[d + # + 3] & @ a

and

Inactivate[d+a+3]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
  • Thanks a lot for your answer. I see that your solution works for the given example. But can a replacement rule be derived from it which can be applied to an arbitrary expression containing an arbitrary number of arbitrarily named symbols which could be replaced by their values? I am working on a function which takes any expression as an argument and should print the requested form. I'm new to Mathematica and don't quite see how the With construction can be transformed into such a replacement rule. – Roland Salz Sep 10 '18 at 19:39
  • @RolandSalz, please see the update. – kglr Sep 11 '18 at 06:19
  • Thanks a lot again for this exhaustive answer! I'll experiment with your proposals and see whether they can cover all the cases I have in mind. – Roland Salz Sep 11 '18 at 19:24