Evaluate Only Part of a Function

Question

I have a list of functions, each containing none or more of the functions Plus, Times, Subtract and Divide. They could be in any arrangement and with any numbers. This is one such example.

HoldForm[Plus[3+Times[7,Subtract[9,Plus[4,5]],Divide[29,Subtract[4,3]]]]]*

There is an error here, The above should read: Plus[3,Times[7

The numbers can be any positive integer. I need to calculate just the Divide and Subtract functions to find out if they evaluate to 1 or 0 respectively as I consider functions in the list that have this property trivial and I want to filter them out.

I am somewhat a beginner with Wolfram/Mathematica code and I have been attempting to extract the Divide and Subtract parts as a list and then calculating just them parts but so-far my attempts at solving this have been totally unfruitful, partly because I can't know beforehand where the Divide or Subtract functions are in the function or how deep they will be.

Is there a way to accomplish this?

Edit: Just to help clarify what I am trying to achieve. I have a list of functions such as

{HoldForm[Plus[3,Times[7,Subtract[9,Plus[4,5]],Divide[29,Subtract[4,3]]]]], HoldForm[Plus[7,Times[2,Divide[16,Subtract[9,Plus[4,1]]]]]], HoldForm[Plus[3,Times[7,9],29]]}

I need to remove the first element from the list because it is a function that divides by 1 (and subtracts 0), making is only trivially different from the 3rd element of the list. After removing the first function I want to display the output like this

{$7+2 \frac{16}{9-(4+1)}$,$3+7\times 9+29$}

Welcome to Mathematica.SE! Can you please put any code snippets in code blocks to improve the readability of the question? — Szabolcs, Sep 13 '18 at 13:05
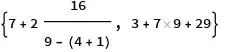
What would be a result of Subtract[9,Plus[4,5]] if Plus is not included in your list? — Kuba, Sep 13 '18 at 13:10
In my example, the whole thing should be removed from my list of functions. This is because Subtract[9,Plus[4,5]] will evaluate to 0 and so it means the example is trivial as there will be another function in the list that is the same except it won't Subtract[0] — RedPython, Sep 13 '18 at 13:19
In that case why don't you just evaluate the whole thing and say that the result is 3? — Szabolcs, Sep 13 '18 at 13:21
Thanks for the advice Szabolcs. Advice appreciated. I have looked up how to do it and will ensure I follow your advice going forward. — RedPython, Sep 13 '18 at 13:21
Also, are you aware that in Mathematica - and / are not represented with Subtract and Divide? Thus unless you explicitly typed in Subtract/Divide, kglr's answer (which I would also have suggested otherwise) will not work. — Szabolcs, Sep 13 '18 at 13:21
I want to display the function unevaluated for the user, but only if the output doesn't contain anything that just means subtract nothing or divide by one — RedPython, Sep 13 '18 at 13:26
Szabolics, I think that is my bad writing skills, I have edited the question to remove the / — RedPython, Sep 13 '18 at 13:29
HoldForm[Plus[3+Times[7,Subtract[9,Plus[4,5]],Divide[29,Subtract[4,3]]]]] should be rejected from my list but HoldForm[Plus[7,Times[2,Divide[16,Subtract[9,Plus[4,1]]]]]] should not. — RedPython, Sep 13 '18 at 13:41
No, that / was not confusing. Let me rephrase: do you work with (1) expressions such as 1/(2+3) or (2) expression like Divide[1, 2+3]? Are you aware that these are not the same thing? Do you really work with the specific function Divide, or do you work with division in general, which may be represented in a different way? — Szabolcs, Sep 13 '18 at 14:03

Sjoerd Smit · Answer 1 · 2018-09-13T14:14:10.273

The answer of kglr works if you only want to do the evaluations associated with Divide and Subtract. If instead you want every subexpression with these head to evaluate completely, use the following trick:

Hold[
  Plus[
   3 + Times[7, Subtract[9, Plus[4, 5]], 
     Divide[29, Subtract[4, 3]]]]
] /. {
   expr : (_Divide | _Subtract) :> With[{x = expr}, x /; True]
}

See also the following answer:

Replacement inside held expression

kglr · Accepted Answer · 2018-09-13T18:24:07.453

Update: Selecting from a list expressions those that do not contain subexpressions that divide by 1 or subtract 0:

list = {HoldForm[Plus[3, Times[7, Subtract[9, Plus[4, 5]], Divide[29, Subtract[4, 3]]]]],
   HoldForm[Plus[7, Times[2, Divide[16, Subtract[9, Plus[4, 1]]]]]],
   HoldForm[Plus[3, Times[7, 9], 29]]};

condition = FreeQ[#, (s_Subtract /; s == 0) | (d_Divide /; d == 1),  ∞] &;
Select[list, condition]

{7 + 2 16/(9 - (4 + 1)), 3 + 7 9 + 29}

Original answer:

exp = Inactivate[Plus[3, Times[7, Subtract[9, Plus[4, 5]], Divide[29, Subtract[4, 3]]]]];
Activate[exp, Divide | Subtract]

3 + 7*(9 - (4 + 5))*29

An alternative way to evaluate completely subexpressions with head Divide or Subtract using RuleCondition (from WReach's answer in the q/a linked in Sjoerd's answer):

HoldForm[Plus[3, Times[7, Subtract[9, Plus[4, 5]], Divide[29, Subtract[4, 3]]]]] /. 
    e : _Subtract | _Divide :> RuleCondition[e]

3 + 7 0 29

Evaluate Only Part of a Function

2 Answers2