Let us solve the system with Floors
sol = Reduce[{4*x1 + 7*x2 + 6*x3 == 186,Floor[(1/2)*x1] + Floor[(1/5)*x2] +
Floor[(1/3)*x3] == 18,Floor[(1/5)*x1] + Floor[(1/2)*x2] + Floor[(1/4)*x3] == 21},
{x1, x2, x3}, Reals]
((155/2 < x1 < 78 && 1/7 (744 - 4 x1) < x2 < 62) || (72 <= x1 <= 73 && 1/7 (714 - 4 x1) < x2 < 62) || (73 < x1 <= 147/2 && 1/7 (714 - 4 x1) < x2 <= 1/7 (726 - 4 x1)) || (147/2 < x1 < 74 && 60 <= x2 <= 1/7 (726 - 4 x1)) || (74 <= x1 < 75 && 1/7 (726 - 4 x1) < x2 < 62) || (153/2 < x1 < 78 && 1/7 (726 - 4 x1) < x2 < 60) || (x1 == 72 && 58 <= x2 < 60) || (72 < x1 < 74 && 58 <= x2 <= 1/7 (708 - 4 x1)) || (75 <= x1 < 76 && 1/7 (714 - 4 x1) < x2 < 60) || (x1 == 74 && 442/7 < x2 < 64) || (74 < x1 < 75 && 1/7 (738 - 4 x1) < x2 <= 1/7 (744 - 4 x1)) || (74 <= x1 < 75 && 1/7 (708 - 4 x1) < x2 <= 1/7 (714 - 4 x1)) || (151/2 < x1 < 76 && 1/7 (708 - 4 x1) < x2 < 58) || (157/2 < x1 < 80 && 1/7 (762 - 4 x1) < x2 < 64) || (68 <= x1 < 137/2 && 56 <= x2 <= 1/7 (666 - 4 x1)) || (x1 == 137/2 && x2 == 56) || (x1 == 70 && 56 < x2 < 58) || (70 < x1 <= 71 && 56 <= x2 < 58) || (71 < x1 < 72 && 56 <= x2 <= 1/7 (690 - 4 x1)) || (70 <= x1 <= 281/4 && 54 <= x2 < 55) || (281/4 < x1 < 72 && 54 <= x2 <= 1/7 (666 - 4 x1))) && x3 == 1/6 (186 - 4 x1 - 7 x2)
and plot it
Region[ImplicitRegion[sol, {x1, x2, x3}]]
Nice. Let us verify it by
FindInstance[{4*x1 + 7*x2 + 6*x3 == 186,
Floor[(1/2)*x1] + Floor[(1/5)*x2] + Floor[(1/3)*x3] == 18,
Floor[(1/5)*x1] + Floor[(1/2)*x2] + Floor[(1/4)*x3] == 21}, {x1, x2, x3}, Reals, 300];
a = {x1, x2, x3} /. %;
ListPlot3D[a, PlotRange -> Full]
At least one of the above results is incorrect. The question arises: which result is true?
Addition. One more different result is obtained by (Many thanks from me to Mariusz Iwaniuk.)
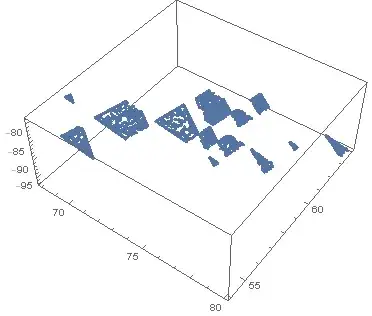
S = FindInstance[{4*x1 + 7*x2 + 6*x3 == 186,
Floor[(1/2)*x1] + Floor[(1/5)*x2] + Floor[(1/3)*x3] == 18,
Floor[(1/5)*x1] + Floor[(1/2)*x2] + Floor[(1/4)*x3] == 21}, {x1, x2, x3},
Reals, 5000, RandomSeeding -> Automatic]; ListPointPlot3D[Evaluate[{x1, x2, x3} /. S],
PlotRange -> Full, PlotStyle -> PointSize[0.01]]


{x1, 2, x3}instead of{x1, x2, x3}as second argument ofReduceso that running it produced the error messageGeneral::ivar. – Henrik Schumacher Sep 16 '18 at 18:27FindInstance[{4*x1 + 7*x2 + 6*x3 == 186, Floor[(1/2)*x1] + Floor[(1/5)*x2] + Floor[(1/3)*x3] == 18, Floor[(1/5)*x1] + Floor[(1/2)*x2] + Floor[(1/4)*x3] == 21}, {x1, x2, x3}, Reals, 10000, RandomSeeding -> Automatic]; a = {x1, x2, x3} /. %; ListPointPlot3D[a, PlotRange -> Full, PlotStyle -> PointSize[0.01]]– Mariusz Iwaniuk Sep 16 '18 at 19:08S = FindInstance[{4*x1 + 7*x2 + 6*x3 == 186, Floor[(1/2)*x1] + Floor[(1/5)*x2] + Floor[(1/3)*x3] == 18, Floor[(1/5)*x1] + Floor[(1/2)*x2] + Floor[(1/4)*x3] == 21}, {x1, x2, x3}, Reals, 10000, RandomSeeding -> Automatic]; ListPointPlot3D[ Evaluate[{x1, x2, x3} /. S], PlotRange -> Full, PlotStyle -> PointSize[0.01]], :) – Mariusz Iwaniuk Sep 16 '18 at 19:28