Options of ContourPlot — poor results when applied to a rapidly varying function

Question

I am struggling to produce a proper vector plot for a certain vector field. In detail, my vector plot is given by the partial derivatives of the function

F[x_, y_] := -(1/x)*(Log[x - y] + 1) + (1/x)*((-y^3/3) + 2)

I add a plot for the reader's convenience

Plot3D[F[x, y], {x, 0.5, 10}, {y, 0, 3}, 
  RegionFunction -> Function[{x, y}, x > y], 
  ColorFunction -> (ColorData["DarkRainbow"][#3] &), 
  PlotRange -> Automatic]

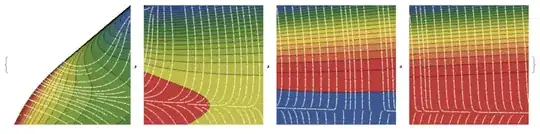
When I try to use StreamPlot

StreamPlot[Evaluate[-D[F[x, y], {{x, y}}]], {x, 0.5, 30}, {y, 0, 3}, 
  StreamStyle -> "Line"];

I get very poor results. I tried with StreamPoints -> Fine,

    StreamPlot[Evaluate[-D[F[x, y], {{x, y}}]], {x, 0.5, 30}, {y, 0, 3}, 
    StreamStyle -> "Line", StreamPoints -> Fine]

but it didn't help

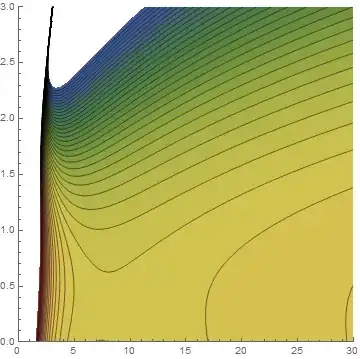
which is clearly a poor representation, e.g. the saddle in the contour plot is not visible at all!

      ContourPlot[F[x, y] , {x, 0.5, 30}, {y, 0, 3}, 
      RegionFunction -> Function[{x, y}, x > y], PlotRange -> Automatic, 
      Contours -> 45, Axes -> True, PlotPoints -> 30, 
      PlotRangePadding -> 0, Frame -> False, 
      ColorFunction -> "DarkRainbow"]

I would like to have many more streamlines, allowing fine details of the surface to be represented.

I wonder if it has something to do with the function having rapidly changing gradients. When I apply the same method to a better behaved function, I get reasonable results.

Any hint would be appreciated.

I can not determine from your question how you want the plot to look. Can you elaborate on what you are aiming for. — m_goldberg, Sep 25 '18 at 23:23
@m_goldberg, I have added some detail, as well as the current status of the plot, which will hopefully make it clear why I am not happy with it. — Smerdjakov, Sep 25 '18 at 23:29
When I evaluate your posted code, I don't get results that look your plots. Please check the posted code against your notebook code. If there are errors in the post, please correct them. — m_goldberg, Sep 25 '18 at 23:41

Alex Trounev · Accepted Answer · 2018-09-26T11:24:19.367

2

The function has a singular point and a logarithmic singularity, so the vector field will be better reproduced in parts, for example

F[x_, y_] := -(1/x)*(Log[x - y] + 1) + (1/x)*((-y^3/3) + 2)



{p1, p2, p3, 
   p4} = {StreamPlot[
    Evaluate[-D[F[x, y], {{x, y}}]], {x, 0.5, 3}, {y, 0, 3}, 
    StreamPoints -> 20, StreamStyle -> LightYellow], 
   StreamPlot[Evaluate[-D[F[x, y], {{x, y}}]], {x, 3, 6}, {y, 0, 3}, 
    StreamPoints -> 20, StreamStyle -> LightYellow], 
   StreamPlot[Evaluate[-D[F[x, y], {{x, y}}]], {x, 6, 9}, {y, 0, 3}, 
    StreamPoints -> 20, StreamStyle -> LightYellow], 
   StreamPlot[Evaluate[-D[F[x, y], {{x, y}}]], {x, 9, 12}, {y, 0, 3}, 
    StreamPoints -> 20, StreamStyle -> LightYellow]};
f = ContourPlot[F[x, y], {x, .5, 12}, {y, 0, 3}, Contours -> 50, 
  ColorFunction -> "DarkRainbow", Frame -> False];
Show[f, p1, p2, p3, p4]

Split the whole picture into separate fragments

{g1, g2, g3, 
  g4} = {ContourPlot[F[x, y], {x, 0.5, 3}, {y, 0, 3}, Contours -> 20, 
   ColorFunction -> "DarkRainbow", Frame -> False], 
  ContourPlot[F[x, y], {x, 3, 6}, {y, 0, 3}, Contours -> 20, 
   ColorFunction -> "DarkRainbow", Frame -> False], 
  ContourPlot[F[x, y], {x, 6, 9}, {y, 0, 3}, Contours -> 20, 
   ColorFunction -> "DarkRainbow", Frame -> False], 
  ContourPlot[F[x, y], {x, 9, 12}, {y, 0, 3}, Contours -> 20, 
   ColorFunction -> "DarkRainbow", Frame -> False]}
 {Show[g1, p1], Show[g2, p2], Show[g3, p3], Show[g4, p4]}

edited Sep 26 '18 at 11:24

answered Sep 26 '18 at 02:02

Alex Trounev

44,369
3
48
106

many thanks for your reply. I am not so sure though why it would be impractical to plot the vector plot over the entire region used for the contour plot in my question, Ultimately I would like to superimpose the vector plot to the countour plot, as done for example in https://mathematica.stackexchange.com/questions/18758/how-do-i-draw-lines-perpendicular-to-contour-lines-on-listplot3d – Smerdjakov Sep 26 '18 at 09:07
ContourPlot also needs to be reproduced in parts. In full scale, it looks awful. – Alex Trounev Sep 26 '18 at 09:40
I see your point, but yet, that might be a little bit subjective. I do not find the Countour Plot that ugly.....and still it should be easy to have nice streamlines flowing perpendicular to the cointour lines...why is it not possible to make the vector plot on the whole region look better? thanks a lot – Smerdjakov Sep 26 '18 at 09:43
I cited a possible model. You can improve it. – Alex Trounev Sep 26 '18 at 10:36
many thanks indeed, very helpful...but now I am left completely puzzled, why are not the sreamlines locally perpendicular to the contour lines?? Thanks again – Smerdjakov Sep 26 '18 at 11:05
This is due to the change in scale in height and width. If we divide the figure into separate fragments of equal width and length, then the perpendicularity of the lines will be restored. I added a picture for illustration. – Alex Trounev Sep 26 '18 at 11:28
Thank you so much. Yet I cannot understand, what change in scale in height and width?? Cannot the same scale be used (is it not used already?) this aspect is really what made me think my plots were incorrect..thanks for the patience – Smerdjakov Sep 26 '18 at 11:31

Options of ContourPlot — poor results when applied to a rapidly varying function

1 Answers1