Using NDSolve for coupled PDE's with moving boundary conditions

Question

im trying to solve numerically a one dimensional case of "Stefan solidification problem". The equations, along with BC's and IC's are:

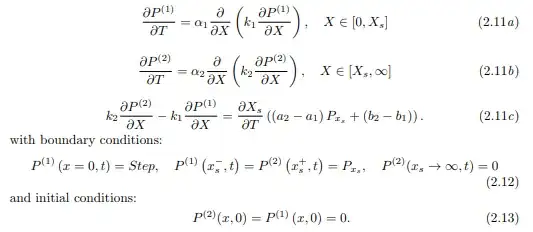
I want to solve for P1(X,T),P2(X,T) and Xs(T) is the moving boundary (P1(Xs,T)=P2(Xs,T)=Const.)

The formulation I have used in Mathematica is:

alpha1 = 3; alpha2 = 7; k1 = 1; k2 = 10; a1 = 14;
a2 = 2; b1 = 1;
b2 = 11; Pxs = 1/2;
sol = NDSolveValue[
{
D[P1[X, T], {T, 1}] - alpha1 D[P1[X, T], {X, 2}] == 0,
D[P2[X, T], {T, 1}] - alpha2 D[P2[X, T], {X, 2}] == 0,
k2 D[P2[X, T], {X, 1}] - k1 D[P1[X, T], {X, 1}] - 
D[Xs[T], {T, 1}] ((a2 - a1) Pxs + (b2 - b1)) == 0,
P1[Xs[T], T] == P2[Xs[T], T],
P1[0, T] == UnitStep[T],
P2[100 , T] == 0,
P2[Xs, T] == Pxs,
P1[X, 0] == 0,
P2[X, 0] == 0},
{P1[X, T], P2[X, T], Xs[T]},
{X, 0, 100},
{T, 0, 1}
]

And I am getting the error massage:

NDSolveValue::conarg: The arguments should be ordered consistently.

How should I define the function "Xs(T)"? or anything else that might help me getting though this will be great. Thanks a lot, Ofek.