What changed in String handling between 11.0 and 11.3?

Question

I was trying to optimize some String-handling code here using my standard trick of converting it to a list of bytes first and using basic list operations instead of the string ones as String* operations used to be very slow.

To my surprise, working with a String is now, amazingly, faster than working with a packed array if you only need to do things like Reverse or Take.

When I looked deeper into what was happening it turns out String is as fast or faster for atomic operations than a packed array of ints is, now.

11.0 Benchmarks

Here's the 11.0 benchmarking:

inpString =
  BlockRandom[
   SeedRandom[0];
   StringJoin@RandomChoice[Alphabet[], 250000]
   ];

inpString // ByteCount

250080

strDats = {#, 
     Mean@Table[First@AbsoluteTiming[StringTake[inpString, {#}]], 
       250]} & /@ Range[1, StringLength@inpString, 500];

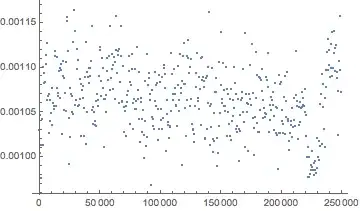
strDats // ListPlot

bytes = ToCharacterCode@inpString;

bytes // ByteCount

2000144

byteDats = {#, First@RepeatedTiming@bytes[[#]]} & /@ 
   Range[1, Length@bytes, 500];

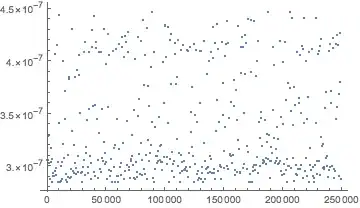
byteDats // ListPlot

And StringTake was incredibly slow relative to Take:

BlockRandom[
  SeedRandom[0];
  ranges = Sort /@ RandomInteger[{1, Length@byteDats}, {500, 2}]
  ];

Map[StringTake[inpString, #] &, ranges] // RepeatedTiming // First

0.539

Map[Take[bytes, #] &, ranges] // RepeatedTiming // First

0.00071

11.3 Results

inpString =
  BlockRandom[
   SeedRandom[0];
   StringJoin@RandomChoice[Alphabet[], 250000]
   ];

inpString // ByteCount

250072

strDats = {#, First@RepeatedTiming[StringTake[inpString, {#}]]} & /@ 
   Range[1, StringLength@inpString, 500];

strDats // ListPlot

bytes = ToCharacterCode@inpString;

bytes // ByteCount

2000144

byteDats = {#, First@RepeatedTiming@bytes[[#]]} & /@ 
   Range[1, Length@bytes, 500];

byteDats // ListPlot

And we see first off that all these element taking operations in String are now much faster. And secondly, it turns out they are ever so slightly faster than the packed array version:

Mean@strDats[[All, 2]]

3.4*10^-7

Mean@byteDats[[All, 2]]

3.8*10^-7

And StringTake is now competitive with Take:

BlockRandom[
  SeedRandom[0];
  ranges = Sort /@ RandomInteger[{1, Length@byteDats}, {500, 2}]
  ];

Map[StringTake[inpString, #] &, ranges] // RepeatedTiming // First

0.00074

Map[Take[bytes, #] &, ranges] // RepeatedTiming // First

0.00065

this combined with the memory efficiency of String means that it can sometimes now be faster to work with strings instead of lists of ints which is wild.

Questions

That was a lot of prologue, but here are my questions:

1. When did this happen?
2. Is there a case where instead of working with a list of ints I should work with the (absolutely meaningless) string instead?
3. How did this happen? (this may be under NDA or something, but I'd be really interested to hear about the internal restructuring that clearly had to take place).