In the paper, entitled:
A Closed Form Solution for the Pull-in Voltage of the Micro Bridge
(Link to PDF: https://pdfs.semanticscholar.org/0d31/33707b1243f6b4e3344c4fa19b831b010b8b.pdf)
... the following equation appears:
I really don't know how to solve this for $\eta_{PI}$, even if all constants are known... do you have any idea ?
EDIT: Mathematica Input: ($n_{PI}$ was replaced with a simple $n$)
The nominator:
nom = Integrate[
b*\[Phi][x]/(g - n*\[Phi][x])^2 +
0.265*b^0.25*\[Phi][x]/(g - n*\[Phi][x])^1.25 +
0.53*h^0.5*\[Phi][x]/(g - n*\[Phi][x])^1.5, {x, 0, L}]
The denominator:
denom = Integrate[
2*b*(\[Phi][x])^2/(g - n*\[Phi][x])^3 +
0.33125*b^0.25*(\[Phi][x])^2/(g - n*\[Phi][x])^2.25 +
0.795*h^0.5*(\[Phi][x])^2/(g - n*\[Phi][x])^2.5, {x, 0, L}]
A typical $ \phi (x)$ function:
\[Phi][x] := a*Sin[x] + b*Cos[x] + c*Sinh[x] + d*Cosh[x]
Some arbitrary constants for numeric solutions to test:
constants = {a->2,b->4,c->7,d->10,g->3,h->2,L->5}
For easier copy-paste:
Clear[\[Phi]]
nom = Integrate[
b*\[Phi][x]/(g - n*\[Phi][x])^2 +
0.265*b^0.25*\[Phi][x]/(g - n*\[Phi][x])^1.25 +
0.53*h^0.5*\[Phi][x]/(g - n*\[Phi][x])^1.5, {x, 0, L}]
denom = Integrate[
2*b*(\[Phi][x])^2/(g - n*\[Phi][x])^3 +
0.33125*b^0.25*(\[Phi][x])^2/(g - n*\[Phi][x])^2.25 +
0.795*h^0.5*(\[Phi][x])^2/(g - n*\[Phi][x])^2.5, {x, 0, L}]
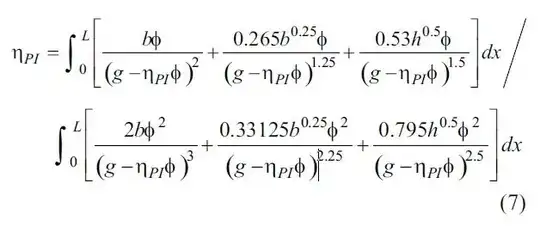
x. You will have to work out what this is and make it explicit. – mikado Oct 06 '18 at 20:02constants = {b->4,b->1}?,decide.bconstant is in meters or micrometers ? – Mariusz Iwaniuk Oct 07 '18 at 09:38ϕ[x]is :ϕ[x] == (Cosh[λ x] - Cos[λ x]) - (Cosh[λ L] - Cos[λ L])/(Sinh[λ L] - Sin[λ L])*(Sinh[λ x] - Sin[λ x])then:λis ? or from eq (3) ?. Solving eq(3) forλthen:λ =0,and thenϕ[x]=0? – Mariusz Iwaniuk Oct 07 '18 at 09:57