Solve integro-differential equations

Question

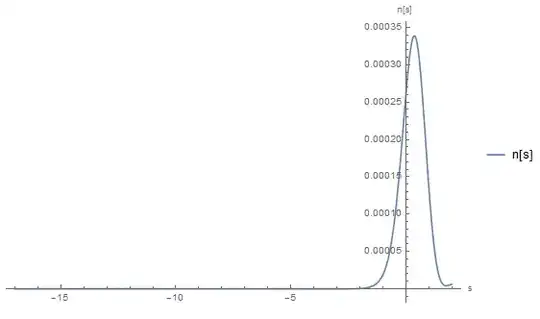
I am trying to numerically solve the following integro-differential equation and get some plots for $n(s)$ vs $s$:

$$ \dot{n}(s)-\frac{\dot{w}(s)}{2w(s)}\int_{-\infty}^s ds'\frac{\dot{w}(s')}{w(s')}(1+2n(s'))\,\cos[2\int_{s'}^s ds'' w(s'')]=0 $$

with $\dot{w}(x)=\frac{dw(x)}{dx}$. The initial condition for $n(s=-\infty)=0$ can be considered and $w(s)$ is a general function of $s$ which one can consider as an example a function like $w(s)=a^2+\sqrt{c-d(1+Tanh[s])}$ with $a,c,d$ constants. I am new in Mathematica that is why I do not have a clear idea where to start. There are some different methods to solve these type of problems in the literature like Adomian, Galerkin methods, etc... but what I have here is a bit more involved than what people used to consider based on those methods...so I thought a numerical solution would be good idea to start with.

MMA code:

w[s_] := a^2 + Sqrt[c - d (1 + Tanh[s])]
Inactivate[n'[s] - w'[s]/(2 w[s])*Integrate[Cos[2 Integrate[w[x], {x, t, s}]]*(w'[t]/
w[t])*(1 + 2 n[t]), {t, -Infinity, s}] == 0, Integrate] // ExpandAll// TeXForm

$\frac{d \text{sech}^2(s) \int _{-\infty }^s\left(-\frac{d \cos \left(2 \int _t^s\left(a^2+\sqrt{c-d-d \tanh (x)}\right)dx\right) \text{sech}^2(t)}{2 \sqrt{c-d-d \tanh (t)} a^2+2 c-2 d-2 d \tanh (t)}-\frac{2 d \cos \left(2 \int _t^s\left(a^2+\sqrt{c-d-d \tanh (x)}\right)dx\right) n(t) \text{sech}^2(t)}{2 \sqrt{c-d-d \tanh (t)} a^2+2 c-2 d-2 d \tanh (t)}\right)dt}{4 a^2 \sqrt{c-d \tanh (s)-d}+4 c-4 d \tanh (s)-4 d}+n'(s)=0$

Answer 1

UPDATE 11.10.2018 for speed-up the code.

w[s_] := a^2 + Sqrt[c - d (1 + Tanh[s])]
D[w[s],s]/ w[s] 

(* -((d Sech[t]^2)/(2 Sqrt[c - d (1 + Tanh[t])] (a^2 + Sqrt[c - d (1 + Tanh[t])]))) *)

Simplifying and putting to integro-differential equation, and next compute integral:

Integrate[w[x], {x, t, s}, Assumptions -> {a > 0, c > d, d > 0, c > 0, t ∈ Reals, s ∈ Reals, s > t}]

(* ? *) 

Mathematica tires to solve and does not give a solution within 1 hour computation.

With Maple 2018.2 I have the answer:

$Version
(* 11.3.0 for Microsoft Windows (64-bit) (March 7, 2018) *)

ClearAll["Global`*"]; Remove["Global`*"];



inf = -17; B = 2;             (* inf is Infinity. With -18 value - > error occurs!! *)
a = 1; c = 3; d = 1;          (* At some c,d values, the integral is divergent *)
steps = 1/100;                           
tolerance = 10^-8;                      

SOL = FixedPointList[Function[n, Module[{INT, int1, n1},
 INT = 
  ParametricNDSolveValue[{int1'[t] == 
     Cos[2*(a^2 s - a^2 t + 
          Sqrt[-c + 2 d]
            ArcTan[Sqrt[c + c E^(2 s) - 2 d E^(2 s)]/(
            Sqrt[-c + 2 d] Sqrt[1 + E^(2 s)])] - 
          Sqrt[-c + 2 d]
            ArcTan[Sqrt[c + c E^(2 t) - 2 d E^(2 t)]/(
            Sqrt[-c + 2 d] Sqrt[1 + E^(2 t)])] - 
          Sqrt[c] ArcTanh[Sqrt[c + c E^(2 s) - 2 d E^(2 s)]/(
            Sqrt[c] Sqrt[1 + E^(2 s)])] + 
          Sqrt[c] ArcTanh[Sqrt[c + c E^(2 t) - 2 d E^(2 t)]/(
            Sqrt[c] Sqrt[1 + E^(2 t)])])]*(-((d Sech[t]^2)/(
        2 Sqrt[c - 
          d (1 + Tanh[t])] (a^2 + Sqrt[
           c - d (1 + Tanh[t])]))))*(1 + 2*n[t]), int1[inf] == 0},
    int1, {t, inf, B}, {s}, PrecisionGoal -> 20];
 NDSolve[{n1'[
       s] - (-((d Sech[s]^2)/(
         4 Sqrt[c - 
           d (1 + Tanh[s])] (a^2 + Sqrt[c - d (1 + Tanh[s])]))))*
       Evaluate[INT[s][s]] == 0, n1[inf] == 0}, n1, {s, inf, B}, 
   PrecisionGoal -> 20][[1, 1, 2]]]],
    Function[s, s], 
SameTest -> (Max[Abs[Table[#1[s] - #2[s], {s, inf, B, steps}]]] < 
   tolerance &)];

Plot[Evaluate[SOL[[-1]][s]], {s, inf, B}, PlotRange -> All, 
PlotLegends -> {"n[s]"}, AxesLabel -> {"s", "n[s]"}]

Numeric errors check:

M[s_] := (SOL[[-1]][s]);

CHECK[s_?NumericQ] := M'[s] - (-((d Sech[s]^2)/(
 4 Sqrt[c - d (1 + Tanh[s])] (a^2 + Sqrt[c - d (1 + Tanh[s])]))))*
NIntegrate[
Cos[2*(a^2 s - a^2 t + 
     Sqrt[-c + 2 d]
       ArcTan[Sqrt[c + c E^(2 s) - 2 d E^(2 s)]/(
       Sqrt[-c + 2 d] Sqrt[1 + E^(2 s)])] - 
     Sqrt[-c + 2 d]
       ArcTan[Sqrt[c + c E^(2 t) - 2 d E^(2 t)]/(
       Sqrt[-c + 2 d] Sqrt[1 + E^(2 t)])] - 
     Sqrt[c] ArcTanh[Sqrt[c + c E^(2 s) - 2 d E^(2 s)]/(
       Sqrt[c] Sqrt[1 + E^(2 s)])] + 
     Sqrt[c] ArcTanh[Sqrt[c + c E^(2 t) - 2 d E^(2 t)]/(
       Sqrt[c] Sqrt[1 + E^(2 t)])])]*(-((d Sech[t]^2)/(
   2 Sqrt[c - 
     d (1 + Tanh[t])] (a^2 + Sqrt[c - d (1 + Tanh[t])]))))*(1 + 
   2*M[t]), {t, inf, s}, 
Method -> {Automatic, "SymbolicProcessing" -> 0}, 
PrecisionGoal -> 20]

Plot[CHECK[s], {s, inf, B}, PlotRange -> All, PlotLegends -> {"n[s]"},
AxesLabel -> {"s", "n[s]"}] // Quiet