Density plot in polar coordinate

Question

I am trying to do a density plot of a function in polar coordinates. The function I am interested in study is
$\Lambda^4 (1 - Cos(\frac{r[t]}{f_r} - \frac{\theta[t]}{f_{\theta}})) + \frac{1}{2} m^2 r[t]^2$

but I don't know how to plot that onto a plane ($r[t]Cos(\theta[t])$, $r[t]Sin(\theta[t])$).

the parameters can be $ f_r = 10^{-3}, f_{\theta} = 10^{-1}, m = 10^{-4}, \Lambda = 10^{-3} $

Any suggestions?

You see, $\Lambda$, $m$, and $f$ are not defined in your post, and you did not clarify what those subscripts for $f$ are intended for. — J. M.'s missing motivation, Oct 08 '18 at 14:00
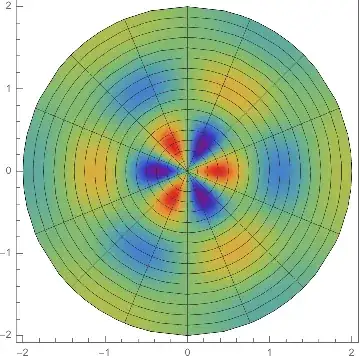
@UlrichNeumann Even better would be to color the plot by height and pick a ViewPoint infinitely above: ParametricPlot3D[{r Cos[t], r Sin[t], f[r, t]}, {r, 0, R}, {t, 0, 2 Pi}, ColorFunction -> "Rainbow", ViewPoint -> {0, 0, Infinity}] — Michael E2, Oct 08 '18 at 14:10
@ Michael E2 Sorry, recognizing your answer , I deleted my comment. Nice idea, thanks. — Ulrich Neumann, Oct 08 '18 at 14:14

Michael E2 · Answer 1 · 2018-10-08T17:05:58.993

One way:

f[r_, t_] := Cos[3 t] Sin[4 r]/(1 + r^2);
DensityPlot[
 f[Sqrt[x^2 + y^2], ArcTan[x, y]], {x, y} ∈ Disk[{0, 0}, 2], 
 Exclusions -> None, PlotPoints -> 50]

Mathematica graphics

Alternative way, based on a deleted comment by @UlrichNeumann:

ParametricPlot3D[{r Cos[t], r Sin[t], f[r, t]},
 {r, 0, 2}, {t, 0, 2 Pi},
 ColorFunction -> "Rainbow", ViewPoint -> {0, 0, Infinity}, 
 Lighting -> {{"Ambient", White}}, BoundaryStyle -> Black, 
 Axes -> {True, True, False}]

Mathematica graphics

Density plot in polar coordinate

1 Answers1