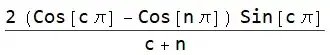Consider the following function:
f = (E^(2 I c \[Phi]) - (E^(2 I \[Phi]))^c) (E^(2 I \[Phi]))^n
Integrating this function with respect to \[Phi] from -\[Pi] to \[Pi] apparently gives:
int1 = Integrate[ f , {\[Phi], -\[Pi], \[Pi]}]
Suppose we would like n to be an integer, so we fully simplify as follows:
Assuming[Element[n, Integers], int1 // FullSimplify]
which, in general, is a non-zero quantity. However, for integer n we should be able to do the integral directly with this assumption in place. This suggests:
int2 = Assuming[Element[n, Integers], Integrate[ f , {\[Phi], -\[Pi], \[Pi]}] ]
0
Now it seems that the integral is actually zero for general integer n! Surely, only one of the two results can be true. Which one is it? And why is Mathematica producing these discrepancies? Is this a bug in Mathematica?