Strange behaviour in derivative of Floor function

Question

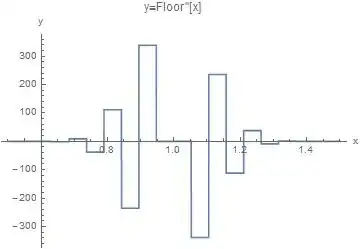
The function Floor[x] is piecewise constant, hence its derivatives should be piecewise zero.

This is far from true in Mathematica

In[497]:= $Version

Out[497]= "10.1.0 for Microsoft Windows (64-bit) (March 24, 2015)"

The first and second derivatives in the interval $\frac{1}{2}\lt x \lt \frac{3}{2}$ are shown in these graphs

Plot[D[Floor[x], {x, 1}] /. x -> xx, {xx, 1/2, 3/2}, PlotRange -> All, 
 PlotLabel -> "y=Floor'[x]", AxesLabel -> {"x", "y"}]

Plot[D[Floor[x], {x, 2}] /. x -> xx, {xx, 1/2, 3/2}, PlotRange -> All,
  PlotLabel -> "y=Floor''[x]", AxesLabel -> {"x", "y"}]

We notice that the drivatives are far from zero even over a broad range of $x$.

In the standard documentation I have found no hint of this problem.

My question: is this a bug?

Mathematica 10.1 is quite old. I see different results than what you describe in more recent versions of the program. — ktm, Oct 10 '18 at 13:18
@ user6014 Thank you for the hint. Could you perhaps show more details in an answer, i.e. how do the plots look in more recent versions? — Dr. Wolfgang Hintze, Oct 10 '18 at 15:19
Did you click on the link that the "this" in my last comment was pointing to? — J. M.'s missing motivation, Oct 10 '18 at 15:56
Thanks, click of "this" reveals that the problem is a dupilcate. In the answer provided here for M11 the bug has been removed. — Dr. Wolfgang Hintze, Oct 10 '18 at 15:59

score 3 · Answer 1 · answered Oct 10 '18 at 15:26

Starting in version M11, Floor'[x] evaluates:

Floor'[x] //TeXForm

$\begin{cases} 0 & x>\lfloor x\rfloor \\ \operatorname{Indeterminate} & \operatorname{True} \end{cases}$

Of course, this obscures the discontinuity at integer x. If you want to produce a derivative that can be integrated back to the original result, you can try using an equivalent HeavisideTheta representation:

{Plot[Floor[x], {x, 1/2, 3/2}], Plot[HeavisideTheta[x-1], {x, 1/2, 3/2}]}

Then:

D[HeavisideTheta[x-1], x]

DiracDelta[-1 + x]

Integrate[DiracDelta[-1+x],x]

HeavisideTheta[-1 + x]

@ Carl Wolf The hint on HeavisideTheta is most useful. It works also in V10. — Dr. Wolfgang Hintze, Oct 10 '18 at 16:01

Strange behaviour in derivative of Floor function

1 Answers1