I am a fresh user of mathematica, soo thank you in advance for your help.
I would like to get a list of points (x,y,z) at any interval (eg every 0.05 by x and y coordinate) which are created by intersection of two "mesh surfaces". The mesh surfaces are created on the basis of a list of points with the coordinates "x, y, z".
I tried to solve it with similar questions info but unfortunately I could not solve the problem. An example of a "similar" task: Finding intersection points of two surfaces (lists)
The data I have:
ODN = {{0, 0, 0}, {0, 1, 0}, {0.16, 0, 0}, {0.16, 1, 0}}
Data = {{0.00, 0.00, -4556460}, {0.00, 0.05, -2946050}, {0.00,
0.10, -1650370}, {0.00, 0.15, -1412950}, {0.00,
0.20, -1187800}, {0.00, 0.25, -1270790}, {0.00,
0.30, -1212100}, {0.00, 0.35, -1277720}, {0.00,
0.40, -1239340}, {0.00, 0.45, -1283850}, {0.00, 0.50, -1247030},
{0.00, 0.55, -1283850}, {0.00, 0.60, -1239340}, {0.00,
0.65, -1277720}, {0.00, 0.70, -1212100}, {0.00, 0.75, -1270790},
{0.00, 0.80, -1187800}, {0.00, 0.85, -1412950}, {0.00,
0.90, -1650370}, {0.00, 0.95, -2946050}, {0.00, 1.00, -4556460},
{0.01, 0.00, -4556460}, {0.01, 0.05, -2946050}, {0.01,
0.10, -1650370}, {0.01, 0.15, -1412950}, {0.01,
0.20, -1187800}, {0.01, 0.25, -1270790},
{0.01, 0.30, -1212100}, {0.01, 0.35, -1277720}, {0.01,
0.40, -1239340}, {0.01, 0.45, -1283850}, {0.01, 0.50, -1247030},
{0.01, 0.55, -1283850}, {0.01, 0.60, -1239340}, {0.01,
0.65, -1277720}, {0.01, 0.70, -1212100}, {0.01, 0.75, -1270790},
{0.01, 0.80, -1187800}, {0.01, 0.85, -1412950}, {0.01,
0.90, -1650370}, {0.01, 0.95, -2946050}, {0.01, 1.00, -4556460},
{0.02, 0.00, -2915090}, {0.02, 0.05, -2009860}, {0.02,
0.10, -904045}, {0.02, 0.15, -608438}, {0.02,
0.20, -463121}, {0.02, 0.25, -467187},
{0.02, 0.30, -475745}, {0.02, 0.35, -477201}, {0.02,
0.40, -497142}, {0.02, 0.45, -486424}, {0.02, 0.50, -503019},
{0.02, 0.55, -486424}, {0.02, 0.60, -497142}, {0.02,
0.65, -477201}, {0.02, 0.70, -475745}, {0.02, 0.75, -467187},
{0.02, 0.80, -463121}, {0.02, 0.85, -608438}, {0.02,
0.90, -904045}, {0.02, 0.95, -2009860}, {0.02, 1.00, -2915090},
{0.03, 0.00, -2104360}, {0.03, 0.05, -1439980}, {0.03,
0.10, -480315}, {0.03, 0.15, -151880}, {0.03, 0.20, -75422}, {0.03,
0.25, -55561},
{0.03, 0.30, -71717}, {0.03, 0.35, -74647}, {0.03,
0.40, -84924}, {0.03, 0.45, -86873}, {0.03, 0.50, -88763},
{0.03, 0.55, -86873}, {0.03, 0.60, -84924}, {0.03,
0.65, -74647}, {0.03, 0.70, -71718}, {0.03, 0.75, -55562},
{0.03, 0.80, -75423}, {0.03, 0.85, -151880}, {0.03,
0.90, -480315}, {0.03, 0.95, -1439980}, {0.03, 1.00, -2104360},
{0.04, 0.00, -1642920}, {0.04, 0.05, -1093510}, {0.04,
0.10, -233040}, {0.04, 0.15, 108786}, {0.04, 0.20, 152277}, {0.04,
0.25, 163757},
{0.04, 0.30, 154681}, {0.04, 0.35, 146344}, {0.04, 0.40,
141116}, {0.04, 0.45, 136596}, {0.04, 0.50, 136802},
{0.04, 0.55, 136596}, {0.04, 0.60, 141116}, {0.04, 0.65,
146344}, {0.04, 0.70, 154681}, {0.04, 0.75, 163757},
{0.04, 0.80, 152277}, {0.04, 0.85, 108786}, {0.04,
0.90, -233041}, {0.04, 0.95, -1093510}, {0.04, 1.00, -1642920},
{0.05, 0.00, -1318010}, {0.05, 0.05, -825356}, {0.05,
0.05, -32726}, {0.05, 0.15, 300576}, {0.05, 0.20, 333127}, {0.05,
0.25, 332415},
{0.05, 0.30, 326069}, {0.05, 0.35, 317267}, {0.05, 0.40,
312293}, {0.05, 0.45, 308919}, {0.05, 0.50, 308124},
{0.05, 0.55, 308919}, {0.05, 0.60, 312293}, {0.05, 0.65,
317267}, {0.05, 0.70, 326069}, {0.05, 0.75, 332415},
{0.05, 0.80, 333127}, {0.05, 0.85, 300576}, {0.05,
0.90, -32726}, {0.05, 0.95, -825356}, {0.05, 1.00, -1318010},
{0.06, 0.00, -1101690}, {0.06, 0.05, -642355}, {0.06, 0.10,
99285}, {0.06, 0.15, 417745}, {0.06, 0.20, 445153}, {0.06, 0.25,
435908},
{0.06, 0.30, 429874}, {0.06, 0.35, 421301}, {0.06, 0.40,
416488}, {0.06, 0.45, 413671}, {0.06, 0.50, 412630},
{0.06, 0.55, 413671}, {0.06, 0.60, 416488}, {0.06, 0.65,
421301}, {0.06, 0.70, 429874}, {0.06, 0.75, 435908},
{0.06, 0.80, 445153}, {0.06, 0.85, 417745}, {0.06, 0.90,
99285}, {0.06, 0.95, -642356}, {0.06, 1.00, -1101690},
{0.07, 0.00, -907645}, {0.07, 0.05, -465041}, {0.07, 0.10,
237750}, {0.07, 0.15, 537641}, {0.07, 0.20, 563065}, {0.07, 0.25,
546859},
{0.07, 0.30, 540332}, {0.07, 0.35, 532225}, {0.07, 0.40,
527426}, {0.07, 0.45, 525032}, {0.07, 0.50, 523932},
{0.07, 0.55, 525032}, {0.07, 0.60, 527426}, {0.07, 0.65,
532225}, {0.07, 0.70, 540332}, {0.07, 0.75, 546859},
{0.07, 0.80, 563065}, {0.07, 0.85, 537641}, {0.07, 0.90,
237750}, {0.07, 0.95, -465042}, {0.07, 1.00, -907645},
{0.08, 0.00, -1052140}, {0.08, 0.05, -614762}, {0.08, 0.10,
80436}, {0.08, 0.15, 376964}, {0.08, 0.20, 401690}, {0.08, 0.25,
384496},
{0.08, 0.30, 377504}, {0.08, 0.35, 369728}, {0.08, 0.40,
364764}, {0.08, 0.45, 362579}, {0.08, 0.50, 361364},
{0.08, 0.55, 362579}, {0.08, 0.60, 364764}, {0.08, 0.65,
369728}, {0.08, 0.70, 377504}, {0.08, 0.75, 384496},
{0.08, 0.80, 401690}, {0.08, 0.85, 376964}, {0.08, 0.90,
80435}, {0.08, 0.95, -614763}, {0.08, 1.00, -1052140},
{0.09, 0.00, -907645}, {0.09, 0.05, -465041}, {0.09, 0.10,
237750}, {0.09, 0.15, 537641}, {0.09, 0.20, 563065}, {0.09, 0.25,
546859},
{0.09, 0.30, 540332}, {0.09, 0.35, 532225}, {0.09, 0.40,
527426}, {0.09, 0.45, 525032}, {0.09, 0.50, 523932},
{0.09, 0.55, 525032}, {0.09, 0.60, 527426}, {0.09, 0.65,
532225}, {0.09, 0.70, 540332}, {0.09, 0.75, 546859},
{0.09, 0.80, 563065}, {0.09, 0.85, 537641}, {0.09, 0.90,
237750}, {0.09, 0.95, -465042}, {0.09, 1.00, -907645},
{0.10, 0.00, -1101690}, {0.10, 0.05, -642355}, {0.10, 0.10,
99285}, {0.10, 0.15, 417745}, {0.10, 0.10, 445153}, {0.10, 0.25,
435908},
{0.10, 0.30, 429874}, {0.10, 0.35, 421301}, {0.10, 0.40,
416488}, {0.10, 0.45, 413671}, {0.10, 0.50, 412630},
{0.10, 0.55, 413671}, {0.10, 0.60, 416488}, {0.10, 0.65,
421301}, {0.10, 0.70, 429874}, {0.10, 0.75, 435908},
{0.10, 0.80, 445153}, {0.10, 0.85, 417745}, {0.10, 0.90,
99285}, {0.10, 0.95, -642356}, {0.10, 1.00, -1101690},
{0.11, 0.00, -1318010}, {0.11, 0.05, -825356}, {0.11,
0.10, -32726}, {0.11, 0.15, 300576}, {0.11, 0.20, 333127}, {0.11,
0.25, 332415},
{0.11, 0.30, 326069}, {0.11, 0.35, 317267}, {0.11, 0.40,
312293}, {0.11, 0.45, 308919}, {0.11, 0.50, 308124},
{0.11, 0.55, 308919}, {0.11, 0.60, 312293}, {0.11, 0.65,
317267}, {0.11, 0.70, 326069}, {0.11, 0.75, 332415},
{0.11, 0.80, 333127}, {0.11, 0.85, 300576}, {0.11,
0.90, -32726}, {0.11, 0.95, -825356}, {0.11, 1.00, -1318010},
{0.12, 0.00, -1642920}, {0.12, 0.05, -1093510}, {0.12,
0.10, -233040}, {0.08, 0.15, 108786}, {0.12, 0.20, 152277}, {0.12,
0.25, 163757},
{0.12, 0.30, 154681}, {0.12, 0.35, 146344}, {0.12, 0.40,
141116}, {0.12, 0.45, 136596}, {0.12, 0.50, 136802},
{0.12, 0.55, 136596}, {0.12, 0.60, 141116}, {0.12, 0.65,
146344}, {0.12, 0.70, 154681}, {0.12, 0.75, 163757},
{0.12, 0.80, 152277}, {0.12, 0.85, 108786}, {0.12,
0.90, -233041}, {0.12, 0.95, -1093510}, {0.12, 1.00, -1642920},
{0.13, 0.00, -2104360}, {0.13, 0.05, -1439980}, {0.13,
0.10, -480315}, {0.13, 0.15, -151880}, {0.13, 0.20, -75422}, {0.13,
0.25, -55561},
{0.13, 0.30, -71717}, {0.13, 0.35, -74647}, {0.13,
0.40, -84924}, {0.13, 0.45, -86873}, {0.13, 0.50, -88763},
{0.13, 0.55, -86873}, {0.13, 0.60, -84924}, {0.13,
0.65, -74647}, {0.13, 0.70, -71718}, {0.13, 0.75, -55562},
{0.13, 0.80, -75423}, {0.13, 0.85, -151880}, {0.13,
0.90, -480315}, {0.13, 0.95, -1439980}, {0.13, 1.00, -2104360},
{0.14, 0.00, -2915090}, {0.14, 0.05, -2009860}, {0.14,
0.10, -904045}, {0.14, 0.15, -608438}, {0.14,
0.20, -463121}, {0.14, 0.25, -467187},
{0.14, 0.30, -475745}, {0.14, 0.35, -477201}, {0.14,
0.40, -497142}, {0.14, 0.45, -486424}, {0.14, 0.50, -503019},
{0.14, 0.55, -486424}, {0.14, 0.60, -497142}, {0.14,
0.65, -477201}, {0.14, 0.70, -475745}, {0.14, 0.75, -467187},
{0.14, 0.80, -463121}, {0.14, 0.85, -608438}, {0.14,
0.90, -904045}, {0.14, 0.95, -2009860}, {0.14, 1.00, -2915090},
{0.15, 0.00, -4556460}, {0.15, 0.05, -2946050}, {0.15,
0.10, -1650370}, {0.15, 0.15, -1412950}, {0.15,
0.20, -1187800}, {0.15, 0.25, -1270790},
{0.15, 0.15, -1212100}, {0.15, 0.35, -1277720}, {0.15,
0.40, -1239340}, {0.15, 0.45, -1283850}, {0.15, 0.50, -1247030},
{0.15, 0.55, -1283850}, {0.15, 0.60, -1239340}, {0.15,
0.65, -1277720}, {0.15, 0.70, -1212100}, {0.15, 0.75, -1270790},
{0.15, 0.80, -1187800}, {0.15, 0.85, -1412950}, {0.15,
0.90, -1650370}, {0.15, 0.95, -2946050}, {0.01, 1.00, -4556460},
{0.16, 0.00, -4556460}, {0.16, 0.05, -2946050}, {0.16,
0.10, -1650370}, {0.16, 0.15, -1412950}, {0.16,
0.20, -1187800}, {0.16, 0.25, -1270790},
{0.16, 0.15, -1212100}, {0.16, 0.35, -1277720}, {0.16,
0.40, -1239340}, {0.16, 0.45, -1283850}, {0.16, 0.50, -1247030},
{0.16, 0.55, -1283850}, {0.16, 0.60, -1239340}, {0.16,
0.65, -1277720}, {0.16, 0.70, -1212100}, {0.16, 0.75, -1270790},
{0.16, 0.80, -1187800}, {0.16, 0.85, -1412950}, {0.16,
0.90, -1650370}, {0.16, 0.95, -2946050}, {0.16, 1.00, -4556460}}
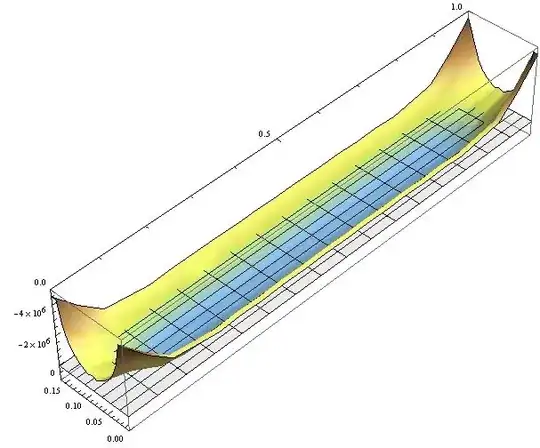
F1 = ListPlot3D[Data, BoxRatios -> {0.16, 1, 0.2},
PlotRange -> {{0, 0.16}, {0, 1}, {1000000, -5000000}}, Mesh -> None,
ColorFunction -> "SouthwestColors"]
F2 = ListPlot3D[ODN, BoxRatios -> {0.16, 1, 0.2},
PlotRange -> {{0, 0.16}, {0, 1}, {1000000, -5000000}},
PlotStyle -> {Gray, Opacity[0.2]}]
Show[F1, F2]
Once again, I will be very grateful for your help.
EDIT I
After tips @kglr I'm almost at the end - unfortunately, on my computer points are displayed differently than in the comment below. Maybe it's the fault of the Mathematica version (I have version 9)?
EDIT II
@kglr solved my problem (tips in the comments). Works well and thank you again @kglr .
EDIT III
Hello Again
welcome back
Unfortunately, I encountered a problem with the solution - if the surface is not convex, the solution above unfortunately does not work. Example below - I have point data:
S22Y01:={{0.005, 0.975, -4098820}, {0.005, 0.925, 1491250}, {0.005,
0.875, -28651}, {0.005, 0.825, -126520}, {0.005,
0.775, -64731}, {0.005, 0.725, -104303}, {0.005,
0.675, -79939}, {0.005, 0.625, -96720}, {0.005,
0.575, -87269}, {0.005, 0.525, -91978}, {0.005,
0.475, -91978}, {0.005, 0.425, -87269}, {0.005,
0.375, -96720}, {0.005, 0.325, -79939}, {0.005,
0.275, -104303}, {0.005, 0.225, -64732}, {0.005,
0.175, -126521}, {0.005, 0.125, -28651}, {0.005, 0.075,
1491250}, {0.005, 0.025, -4098820}, {0.015,
0.975, -4697260}, {0.015, 0.925, 1827450}, {0.015, 0.875,
32231}, {0.015, 0.825, -77745}, {0.015, 0.775, -9879}, {0.015,
0.725, -54141}, {0.015, 0.675, -26396}, {0.015,
0.625, -44977}, {0.015, 0.575, -34275}, {0.015,
0.525, -39468}, {0.015, 0.475, -39468}, {0.015,
0.425, -34275}, {0.015, 0.375, -44978}, {0.015,
0.325, -26396}, {0.015, 0.275, -54141}, {0.015,
0.225, -9879}, {0.015, 0.175, -77745}, {0.015, 0.125,
32231}, {0.015, 0.075, 1827460}, {0.015, 0.025, -4697260}, {0.025,
0.975, -3973280}, {0.025, 0.925, 1528990}, {0.025, 0.875,
69598}, {0.025, 0.825, -32712}, {0.025, 0.775, 29682}, {0.025,
0.725, -11319}, {0.025, 0.675, 14488}, {0.025,
0.625, -2641}, {0.025, 0.575, 7329}, {0.025, 0.525, 2533}, {0.025,
0.475, 2533}, {0.025, 0.425, 7329}, {0.025, 0.375, -2642}, {0.025,
0.325, 14487}, {0.025, 0.275, -11319}, {0.025, 0.225,
29682}, {0.025, 0.175, -32712}, {0.025, 0.125, 69598}, {0.025,
0.075, 1528990}, {0.025, 0.025, -3973280}, {0.035,
0.975, -3699430}, {0.035, 0.925, 1434040}, {0.035, 0.875,
71368}, {0.035, 0.825, -18771}, {0.035, 0.775, 35147}, {0.035,
0.725, -92}, {0.035, 0.675, 21944}, {0.035, 0.625, 7239}, {0.035,
0.575, 15798}, {0.035, 0.525, 11659}, {0.035, 0.475, 11659}, {0.035,
0.425, 15798}, {0.035, 0.375, 7239}, {0.035, 0.325, 21943}, {0.035,
0.275, -93}, {0.035, 0.225, 35146}, {0.035, 0.175, -18771}, {0.035,
0.125, 71369}, {0.035, 0.075, 1434050}, {0.035,
0.025, -3699430}, {0.045, 0.975, -2556970}, {0.045, 0.925,
589167}, {0.045, 0.875, 68270}, {0.045, 0.825, -13121}, {0.045,
0.775, 34969}, {0.045, 0.725, 3117}, {0.045, 0.675, 23125}, {0.045,
0.625, 9696}, {0.045, 0.575, 17541}, {0.045, 0.525, 13739}, {0.045,
0.475, 13739}, {0.045, 0.425, 17541}, {0.045, 0.375, 9695}, {0.045,
0.325, 23125}, {0.045, 0.275, 3117}, {0.045, 0.225, 34969}, {0.045,
0.175, -13122}, {0.045, 0.125, 68270}, {0.045, 0.075,
589168}, {0.045, 0.025, -2556970}, {0.055, 0.975, -1734810}, {0.055,
0.925, -89464}, {0.055, 0.875, 63625}, {0.055,
0.825, -10042}, {0.055, 0.775, 33048}, {0.055, 0.725, 4086}, {0.055,
0.675, 22283}, {0.055, 0.625, 10028}, {0.055, 0.575,
17193}, {0.055, 0.525, 13719}, {0.055, 0.475, 13719}, {0.055, 0.425,
17193}, {0.055, 0.375, 10028}, {0.055, 0.325, 22282}, {0.055,
0.275, 4086}, {0.055, 0.225, 33047}, {0.055, 0.175, -10042}, {0.055,
0.125, 63625}, {0.055, 0.075, -89463}, {0.055,
0.025, -1734810}, {0.065, 0.975, -1631200}, {0.065,
0.925, -85660}, {0.065, 0.875, 58998}, {0.065,
0.825, -10133}, {0.065, 0.775, 30128}, {0.065, 0.725, 2769}, {0.065,
0.675, 19914}, {0.065, 0.625, 8375}, {0.065, 0.575, 15113}, {0.065,
0.525, 11850}, {0.065, 0.475, 11850}, {0.065, 0.425,
15113}, {0.065, 0.375, 8375}, {0.065, 0.325, 19914}, {0.065, 0.275,
2769}, {0.065, 0.225, 30128}, {0.065, 0.175, -10133}, {0.065, 0.125,
58998}, {0.065, 0.075, -85660}, {0.065, 0.025, -1631200}, {0.075,
0.975, -1580130}, {0.075, 0.925, -85180}, {0.075, 0.875,
55136}, {0.075, 0.825, -11562}, {0.075, 0.775, 27188}, {0.075,
0.725, 678}, {0.075, 0.675, 17272}, {0.075, 0.625, 6101}, {0.075,
0.575, 12623}, {0.075, 0.525, 9466}, {0.075, 0.475, 9466}, {0.075,
0.425, 12623}, {0.075, 0.375, 6101}, {0.075, 0.325, 17272}, {0.075,
0.275, 677}, {0.075, 0.225, 27188}, {0.075, 0.175, -11562}, {0.075,
0.125, 55136}, {0.075, 0.075, -85180}, {0.075,
0.025, -1580130}, {0.085, 0.975, -1580130}, {0.085,
0.925, -85180}, {0.085, 0.875, 55136}, {0.085,
0.825, -11562}, {0.085, 0.775, 27188}, {0.085, 0.725, 678}, {0.085,
0.675, 17272}, {0.085, 0.625, 6101}, {0.085, 0.575, 12623}, {0.085,
0.525, 9466}, {0.085, 0.475, 9466}, {0.085, 0.425, 12623}, {0.085,
0.375, 6101}, {0.085, 0.325, 17272}, {0.085, 0.275, 677}, {0.085,
0.225, 27188}, {0.085, 0.175, -11562}, {0.085, 0.125,
55136}, {0.085, 0.075, -85180}, {0.085, 0.025, -1580130}, {0.095,
0.975, -1631200}, {0.095, 0.925, -85660}, {0.095, 0.875,
58998}, {0.095, 0.825, -10133}, {0.095, 0.775, 30128}, {0.095,
0.725, 2769}, {0.095, 0.675, 19914}, {0.095, 0.625, 8375}, {0.095,
0.575, 15113}, {0.095, 0.525, 11850}, {0.095, 0.475, 11850}, {0.095,
0.425, 15113}, {0.095, 0.375, 8375}, {0.095, 0.325, 19914}, {0.095,
0.275, 2769}, {0.095, 0.225, 30128}, {0.095,
0.175, -10133}, {0.095, 0.125, 58998}, {0.095,
0.075, -85660}, {0.095, 0.025, -1631200}, {0.105,
0.975, -1734810}, {0.105, 0.925, -89464}, {0.105, 0.875,
63625}, {0.105, 0.825, -10042}, {0.105, 0.775, 33048}, {0.105,
0.725, 4086}, {0.105, 0.675, 22283}, {0.105, 0.625, 10028}, {0.105,
0.575, 17193}, {0.105, 0.525, 13719}, {0.105, 0.475, 13719}, {0.105,
0.425, 17193}, {0.105, 0.375, 10028}, {0.105, 0.325,
22282}, {0.105, 0.275, 4086}, {0.105, 0.225, 33047}, {0.105,
0.175, -10042}, {0.105, 0.125, 63625}, {0.105,
0.075, -89463}, {0.105, 0.025, -1734810}, {0.115,
0.975, -2556970}, {0.115, 0.925, 589167}, {0.115, 0.875,
68270}, {0.115, 0.825, -13121}, {0.115, 0.775, 34969}, {0.115,
0.725, 3117}, {0.115, 0.675, 23125}, {0.115, 0.625, 9696}, {0.115,
0.575, 17541}, {0.115, 0.525, 13739}, {0.115, 0.475, 13739}, {0.115,
0.425, 17541}, {0.115, 0.375, 9695}, {0.115, 0.325, 23125}, {0.115,
0.275, 3117}, {0.115, 0.225, 34969}, {0.115,
0.175, -13122}, {0.115, 0.125, 68270}, {0.115, 0.075,
589168}, {0.115, 0.025, -2556970}, {0.125, 0.975, -3699430}, {0.125,
0.925, 1434040}, {0.125, 0.875, 71368}, {0.125,
0.825, -18771}, {0.125, 0.775, 35147}, {0.125, 0.725, -92}, {0.125,
0.675, 21944}, {0.125, 0.625, 7239}, {0.125, 0.575, 15798}, {0.125,
0.525, 11659}, {0.125, 0.475, 11659}, {0.125, 0.425, 15798}, {0.125,
0.375, 7239}, {0.125, 0.325, 21943}, {0.125, 0.275, -93}, {0.125,
0.225, 35146}, {0.125, 0.175, -18771}, {0.125, 0.125,
71369}, {0.125, 0.075, 1434050}, {0.125, 0.025, -3699430}, {0.135,
0.975, -3973280}, {0.135, 0.925, 1528990}, {0.135, 0.875,
69598}, {0.135, 0.825, -32712}, {0.135, 0.775, 29682}, {0.135,
0.725, -11319}, {0.135, 0.675, 14488}, {0.135,
0.625, -2641}, {0.135, 0.575, 7329}, {0.135, 0.525, 2533}, {0.135,
0.475, 2533}, {0.135, 0.425, 7329}, {0.135, 0.375, -2642}, {0.135,
0.325, 14487}, {0.135, 0.275, -11319}, {0.135, 0.225,
29682}, {0.135, 0.175, -32712}, {0.135, 0.125, 69598}, {0.135,
0.075, 1528990}, {0.135, 0.025, -3973280}, {0.145,
0.975, -4697260}, {0.145, 0.925, 1827450}, {0.145, 0.875,
32231}, {0.145, 0.825, -77745}, {0.145, 0.775, -9879}, {0.145,
0.725, -54141}, {0.145, 0.675, -26396}, {0.145,
0.625, -44977}, {0.145, 0.575, -34275}, {0.145,
0.525, -39468}, {0.145, 0.475, -39468}, {0.145,
0.425, -34275}, {0.145, 0.375, -44978}, {0.145,
0.325, -26396}, {0.145, 0.275, -54141}, {0.145,
0.225, -9879}, {0.145, 0.175, -77745}, {0.145, 0.125,
32231}, {0.145, 0.075, 1827460}, {0.145, 0.025, -4697260}, {0.155,
0.975, -4098820}, {0.155, 0.925, 1491250}, {0.155,
0.875, -28651}, {0.155, 0.825, -126520}, {0.155,
0.775, -64731}, {0.155, 0.725, -104303}, {0.155,
0.675, -79939}, {0.155, 0.625, -96720}, {0.155,
0.575, -87269}, {0.155, 0.525, -91978}, {0.155,
0.475, -91978}, {0.155, 0.425, -87269}, {0.155,
0.375, -96720}, {0.155, 0.325, -79939}, {0.155,
0.275, -104303}, {0.155, 0.225, -64732}, {0.155,
0.175, -126521}, {0.155, 0.125, -28651}, {0.155, 0.075,
1491250}, {0.155, 0.025, -4098820}}
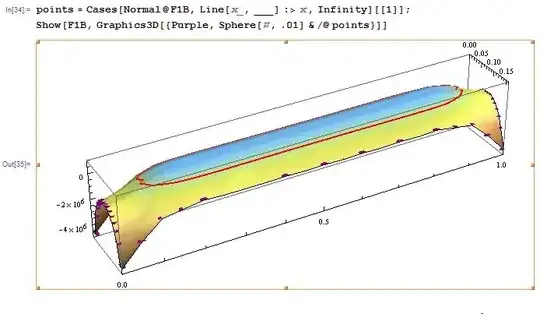
After displaying and using the "cases" function, I get intersection points for only one line of interesction. I guess why this is so - unfortunately I do not know how to get points from all intersection lines.
S22Y1PLOT =
ListPlot3D[S22Y1, BoxRatios -> {0.16, 1, 0.2},
PlotRange -> {{0, 0.16}, {0, 1}, {1000000, -5000000}},
BoundaryStyle -> None, MeshFunctions -> {#3 &},
Mesh -> {{{0, Directive[Thick, Red]}}},
ColorFunction -> "SouthwestColors"]
Y01POINTS = Cases[Normal@S22Y1PLOT, Line[x_, ___] :> x, Infinity][[1]];
Show[S22Y1PLOT, Graphics3D[{Purple, Sphere[#, .01] & /@ Y01POINTS}]]
Is it possible to get points from all lines of intersection? Maybe @kglr ? You've done great job with the previous problem :)