Using NDSolve with conditional expression

Question

I am trying to solve the 2nd order ODE for a harmonic oscillator under the influence of a harmonic restoring force, a sliding friction force, and a static friction force. My equations are below:

$$ x''(t) = \frac{-A}{M}-\frac{B}{M}\,\frac{x'(t)}{|x'(t)|},\quad |x'(t)|>0$$ $$ x''(t) = \frac{-A}{M}+K, \quad |x'(t)|=0$$

I have attempted to implement this in Mathematica using the following code:

s = 
  NDSolve[
    {x''[t] == 
       -(A/M) x[t] + 
         Piecewise[{{K, Abs[x'[t]] <= ϵ}, {-B/M Sign[x'[t]], Abs[x'[t]] > ϵ}}],
    x[0] == x0, x'[0] == v0},
    x, {t, 0, Tmax}];

I have also tried to use If instead of Piecewise and neither have worked. I am getting an error that a singularity or stiff system is suspected.

I have implemented RK4 in MATLAB for this system, but wish to do it in Mathematica (I am fairly new).

I assume that I am inputting the equations wrong. How should I structure my equation for $x''(t)$ so that NDSolve is able to function properly?

I know the correct behavior of the system -- the mass will oscillate as a dampened system and come to rest within $x(t)=\pm \frac{K}{A}$ range.

NDSolve seems to have issues when my mass attempts to move to $x(t) < 0$ and I am unsure why.

I initialize my values as such:

(* Initialize values for simulatin *) 
ϵ := 0.5 $MachineEpsilon (* threshold for |x'[t]| being 0 *)
x0 := 1 (* Starting position *)
v0 := 2 (* Starting velocity *)
A := 0.3 (* Spring Constant *)
B := 0.5 (* Magnitude of Sliding Friction *)
K := 0.2 (* Magnitude of Static Friction *)
M := 1 (* Mass of oscillator *) \
Tmax := 10 (* End of simulation time *)

Edit 1

I am sure there is an answer somewhere on Mathematica StackExchange, but after hours of searching, I have not found anything.

Edit 2

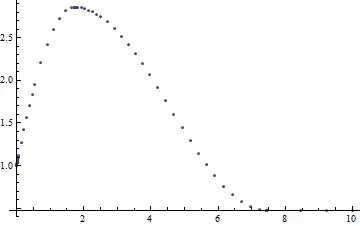
I have made epsilon larger than $MachineEpsilon as should have been very obvious. However when I run the simulation again after t = ~7.45 seconds it explodes to -Infinity... I still do not understand why the system would not oscillate as it should. Possibly this is too much for the NDSolve to handle itself? I have done manually programmed RK4 for this system and it works as expected -- I wanted to reproduce the results in Mathematica to investigate more complicated oscillatory systems.

K is a system-reserved symbol, so please avoid using it. – J. M.'s missing motivation Oct 12 '18 at 00:59 — J. M.'s missing motivation, Oct 12 '18 at 00:59

score 3 · Accepted Answer · answered Oct 12 '18 at 00:05

3

I think your main problem is demanding that ϵ be smaller than $MachineEpsilon. When I rewrite your code as

ϵ = .00001;
x0 = 1;
v0 = 2; 
A = 0.3; 
B = 0.5;
K = 0.2; 
M = 1;
Tmax = 10;

xF = 
  NDSolveValue[
    {x''[t] == -(A/M) x[t] + 
       Piecewise[{{K, Abs[x'[t]] <= ϵ}, {-B/M Sign[x'[t]], Abs[x'[t]] > ϵ}}], 
     x[0] == x0, x'[0] == v0}, 
    x, {t, 0, Tmax}]

I very quickly get

which plots like this.

Plot[xF[t], {t, 0, Tmax}]

answered Oct 12 '18 at 00:05

m_goldberg

107,779
16
103
257

Ugh long day.... I wanted something greater than $MachineEpsilon... Thank you for pointing that out. The system should oscillate past $x(t) = 0$ though. Why does this system not? (Note without static friction it does) – Connor Fuhrman Oct 12 '18 at 01:45
1

@C. Fuhrman Just put A = 3, then there will be oscillations. – Alex Trounev Oct 12 '18 at 03:32

score 3 · Answer 2 · answered Oct 12 '18 at 14:55

Rule of thumb: In many cases, NDSolve handles piecewise function expressed as combination of UnitStep better.

{ϵ = $MachineEpsilon/10, x0 = 1, v0 = 2, A = .3, B = 0.5, k = 0.2, M = 1, Tmax = 10};

rhs = -A/M x[t] + 
   Simplify`PWToUnitStep@
    PiecewiseExpand[
     Piecewise[{{k, Abs[x'[t]] <= ϵ}, {-B/M Sign[x'[t]], Abs[x'[t]] > ϵ}}], Reals];
s = NDSolveValue[{x''[t] == rhs, x[0] == x0, x'[0] == v0}, x, {t, 0, Tmax}]

ListPlot[s, PlotRange -> All]

Mathematica graphics

Reference:

https://mathematica.stackexchange.com/search?q=Simplify%5C%60PWToUnitStep

Easy way to plot ODE solutions from NDSolve?

Using NDSolve with conditional expression

Edit 1

Edit 2

2 Answers2