Finding all roots of a function within an interval

Question

I have the following code:

    a = 200*10^-6;
    Subscript[n, s] = 1.456;
    k = (2*Pi)/\[Lambda];
    l = Round[2*Pi*a/(685*10^-9)];
    \[Beta] = Sqrt[l*(l + 1)]/a;
    \[Alpha] = Sqrt[\[Beta]^2 - k^2];
    F = (\[Alpha] + l/a)*SphericalBesselJ[l, k*Subscript[n, s]*a];
    G = k*Subscript[n, s]*SphericalBesselJ[l + 1, k*Subscript[n, s]*a];
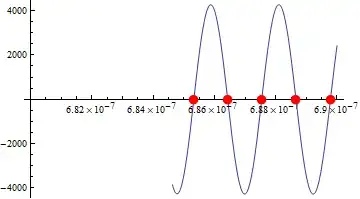
    Plot[F - G, {\[Lambda], 680*10^-9, 690*10^-9}]

It yields an oscillating for a given parameter "a". I want to find all instances in which F=G within the interval in the plot and save the results in a list. I've tried all main root finder functions but none seem to work. How can I do that?

Have you tried NSolve[equation && 680*10^-9 < \[Lambda] < 690*10^-9, \[Lambda]]? — Michael E2, Oct 17 '18 at 23:13
As long as you include the interval as a constraint (as shown by @MichaelE2 for NSolve), either Solve or Reduce will also return the roots. However they will be expressed as Root objects. — Bob Hanlon, Oct 18 '18 at 00:03

score 0 · Accepted Answer · answered Oct 18 '18 at 00:21

As @Michael E2 pointed out in the comments, you can use NSolve.

MapThread[Set, {{a, ns, l, \[Beta]}, {200*10^-6, 1.456, Round[2*Pi*a/(685*10^-9)], Sqrt[l*(l + 1)]/a}}]
k[\[Lambda]_] := (2*Pi)/\[Lambda]
\[Alpha][\[Lambda]_] := Sqrt[\[Beta]^2 - k[\[Lambda]]^2]
F[\[Lambda]_] := (\[Alpha][\[Lambda]] + l/a)*SphericalBesselJ[l, k[\[Lambda]]*ns*a]
G[\[Lambda]_] := k[\[Lambda]]*ns*SphericalBesselJ[l + 1, k[\[Lambda]]*ns*a]
pts = {\[Lambda], 0} /. NSolve[F[\[Lambda]] == G[\[Lambda]] && 680*10^-9 < \[Lambda] < 690*10^-9, \[Lambda]]
Plot[
 F[\[Lambda]] - G[\[Lambda]],
 {\[Lambda], 680*10^-9, 690*10^-9}, 
 Epilog -> {PointSize[.03], Red, Point@pts}
]

{1/5000, 1.456, 1835, 30000 Sqrt[93585]}

{{6.85326*10^-7, 0}, {6.8643*10^-7, 0}, {6.87541*10^-7, 0}, {6.8866*10^-7, 0}, {6.89784*10^-7, 0}}

where the root solutions are

rootsolutions = pts[[;;,1]]

Finding all roots of a function within an interval

1 Answers1