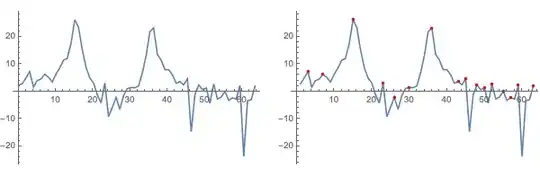
I want to find dominant frequencies of periodogram exactly.
data = Table[5*Sin[0.241*Pi*n ] +3.7*Sin[0.555*Pi*n] + RandomReal[{-1, 1}], {n, 0, 127}];
Periodogram[data]
For example in this signal we have 2 dominant frequency (0.241/2,0.555/2). I have a signal with more frequencies that i need find them with high accuracy. I want to know local maximums of every periodogram and in addition sign this points on periodogram plot. please show me a way. Thank you very much.