How to control boundary markers for overlapping FEM meshes?

Question

I am trying to create FE meshes from vector or bitmap images and have come across the following issue. This is best shown using the following simplified code.

Needs["NDSolve`FEM`"]
coords = {{0., 0.}, {0., 1.}, {1., 1.}, {1., 0.}, {0.5, 0.25}, {1.0, 0.25}, {1.0, 0.75}, {0.5, 0.75}};
ellist = {{1, 2}, {2, 3}, {3, 4}, {4, 1}, {5, 6}, {6, 7}, {7, 8}, {8,5}};
labels = {1, 1, 1, 1, 2, 2, 2, 2};
meshtest = ToBoundaryMesh["Coordinates" -> coords, "BoundaryElements" -> {LineElement[ellist, labels]}];

Ideally I would like to have the inner rectangles boundary labeled with one value and the outer one with another value. However when the elements are co-linear (or rather one is found within another), then the labelling does not work.

meshtest["Wireframe"["MeshElement" -> "BoundaryElements", "MeshElementMarkerStyle" -> Blue]] 

I think this is probably still a desired feature in the boundary meshing algorithm, but is there anyway to find (and solve) these problems automatically, when I don't know a priori whether there is an overlap in the different regions? The images that I am meshing are rather complex and therefore it is difficult to know whether lines overlap or not.

Answer 1

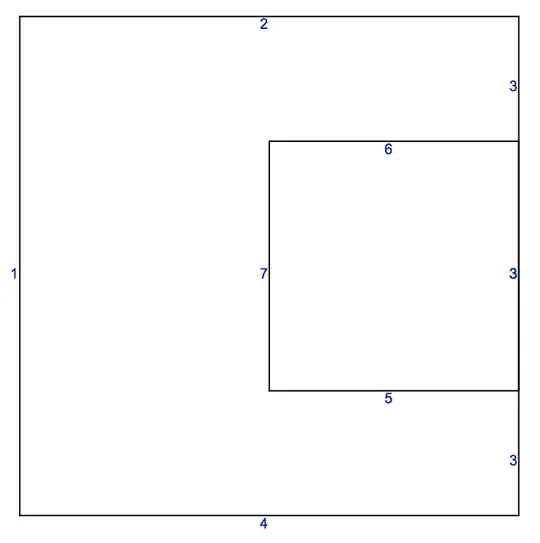
In principle you'd like an input where the overlap is split and specify the markers at the edges like so:

Needs["NDSolve`FEM`"]
coords = {{0., 0.}, {0., 1.}, {1., 1.}, {1., 0.}, {0.5, 0.25}, {1.0, 
    0.25}, {1.0, 0.75}, {0.5, 0.75}};
ellist = {{1, 2}, {2, 3}, {3, 7}, {6, 4}, {4, 1}, {5, 6}, {6, 7}, {7, 
    8}, {8, 5}};
labels = {1, 1, 1, 1, 1, 2, 2, 2, 2};
meshtest = 
  ToBoundaryMesh["Coordinates" -> coords, 
   "BoundaryElements" -> {LineElement[ellist, labels]}];
meshtest["Wireframe"["MeshElement" -> "BoundaryElements", 
  "MeshElementMarkerStyle" -> Blue]]

Now, that may not always be easily possible. In that case you can use the boundary marker function to specify what you want:

(* original data *)
coords = {{0., 0.}, {0., 1.}, {1., 1.}, {1., 0.}, {0.5, 0.25}, {1.0, 
    0.25}, {1.0, 0.75}, {0.5, 0.75}};
ellist = {{1, 2}, {2, 3}, {3, 4}, {4, 1}, {5, 6}, {6, 7}, {7, 8}, {8, 
    5}};
labels = {1, 1, 1, 1, 2, 2, 2, 2};

You'd then specify a boundary marker function (see Options section in ToBoundaryMesh ref page)

boundaryMarkerFunction = 
  Compile[{{boundaryElementCoords, _Real, 
     3}, {pointMarkers, _Integer, 2}},
   MapThread[Module[{pt1 = #[[1]], pt2 = #[[2]]},
      Print[" boundary element coords: ", #1, "  Point markers: ", #2];
      Which[
       pt1[[1]] > 0.9 && pt2[[1]] > 0.9, 2,
       pt1[[1]] < 0.1 && pt2[[1]] < 0.1, 3,
       True, 4 ]] &, {boundaryElementCoords, pointMarkers}]];

Generating the boundary mesh then gives:

meshtest = 
  ToBoundaryMesh["Coordinates" -> coords, 
   "BoundaryElements" -> {LineElement[ellist, labels]}
   , "BoundaryMarkerFunction" -> boundaryMarkerFunction
   ];
SequenceForm[" boundary element coords: ", {{0., 0.}, {0., 1.}}, "  \
Point markers: ", {0, 0}]
SequenceForm[" boundary element coords: ", {{0., 1.}, {1., 1.}}, "  \
Point markers: ", {0, 0}]
SequenceForm[" boundary element coords: ", {{1., 1.}, {1., 0.75}}, "  \
Point markers: ", {0, 0}]
SequenceForm[" boundary element coords: ", {{1., 0.75}, {1., 0.25}}, \
"  Point markers: ", {0, 0}]
SequenceForm[" boundary element coords: ", {{1., 0.25}, {1., 0.}}, "  \
Point markers: ", {0, 0}]
SequenceForm[" boundary element coords: ", {{1., 0.}, {0., 0.}}, "  \
Point markers: ", {0, 0}]
SequenceForm[" boundary element coords: ", {{0.5, 0.25}, {1., 0.25}}, \
"  Point markers: ", {0, 0}]
SequenceForm[" boundary element coords: ", {{1., 0.25}, {1., 0.75}}, \
"  Point markers: ", {0, 0}]
SequenceForm[" boundary element coords: ", {{1., 0.75}, {0.5, 0.75}}, \
"  Point markers: ", {0, 0}]
SequenceForm[" boundary element coords: ", {{0.5, 0.75}, {0.5, \
0.25}}, "  Point markers: ", {0, 0}]

Looking at the mesh:

meshtest["Wireframe"["MeshElement" -> "BoundaryElements", 
  "MeshElementMarkerStyle" -> Blue]]

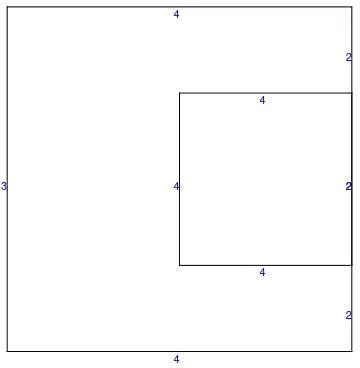
With this approach very general marker distributions should be possible.