Solving non-linear PDEs

Question

I wish to solve the equation

$$\frac{dp(x,y,t)}{dt} = D\ \nabla^2 (p(x,y,t)) -C \ p(x,y,t) - R \ p(x,y,t)^2 $$

But, I get the error

NDSolveValue::femnonlinear: Nonlinear coefficients are not supported in this version of NDSolve.

Now, there are some solutions to this problem which suggest building your own PDE solver, such as 1 and 2. I really don't want to be messing around with making my own PDE solver. Thus, my question

Is there a way I can amend my code below to solve the question?
Can I use Matlab solvePDE, or any other solver, called from Mathematica to solve the PDE?

Minimum "working" example

(*generate data*)

d = MultinormalDistribution[{1, 1}, {{2, -1/3}, {-1/3, 2/3}}];
data = Table[PDF[d, {x, y}], {x, -5, 5}, {y, -5, 5}];
dataintime = Table[data/(1.2^(t)), {t, 0, 10, 1}];
Animate[ListPlot3D[dataintime[[j]], 
  PlotRange -> {{1, 10}, {1, 10}, {0, 0.15}}], {j, 1, 10, 1}]
dataall = dataintime;
data = dataintime[[1]];


(* find fit *) 
data3D = Flatten[MapIndexed[{#2[[1]], #2[[2]], #1} &, data, {2}], 1];
fm = NonlinearModelFit[
  data3D, (1/(2*Pi*sigx*sigy))*
   Exp[(-(((x - ux)^2)/(2*sigx^2) + ((y - uy)^2)/(2*sigy^2)))], {{ux, 
    7}, {uy, 7}, {sigx}, {sigy}}, {x, y}]


(* put in coefficients *) 
coeff1 = 2;
coeff2 = 2;
coeff3 = 2;

(* this equation will work as it has been linearised 
eq1=Derivative[0,0,1][p][x,y,t]\[Equal]coeff1*Laplacian[p[x,y,t],{x,y}\
]-coeff2*p[x,y,t]; *) 

(* equation to solve *) 
eq2 = Derivative[0, 0, 1][p][x, y, t] == 
   coeff1*Laplacian[p[x, y, t], {x, y}] - coeff2*p[x, y, t] - 
    coeff3*p[x, y, t]^2;

(*initial conditions*)
ic = {p[x, y, 0] == fm[x, y]};

(*boundary conditions*)

bcs = {p[0, y, t] == fm[0, 0], p[11, y, t] == 0};

Dynamic["time: " <> ToString[CForm[currentTime]]]; s3D = 
 NDSolveValue[{eq2, ic, bcs}, p, {x, 0, 11}, {y, 0, 11}, {t, 0, 10}, 
  Method -> {"MethodOfLines", 
    "SpatialDiscretization" -> {"FiniteElement", 
      "MeshOptions" -> {"MaxCellMeasure" -> 0.01}}}, 
  EvaluationMonitor :> (currentTime = t;)];

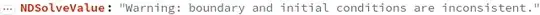
In general, you can use MethodOfLines that enables you to overcome the limitation and solve the nonlinear PDEs provided it is time-dependent. In principle, you already use it. I would omit all details of spatial discretization and mesh options. They may give a conflict and only use Method->MethodOfLines. It worked with your equation for me. If this still gives rise to error message, I would assume that the problem in the way you define the boundary and initial conditions. In the last issue of Mathematica Journal I published a paper, where I solved an alike equation. Have a look. — Alexei Boulbitch, Nov 06 '18 at 10:15
You could solve your problem iterativly: "Using NDSolve iteratively to solve a B" — Ulrich Neumann, Nov 06 '18 at 10:16

score 4 · Answer 1 · edited Jun 16 '20 at 09:23

4

In principal you can do that with:

Dynamic["time: " <> ToString[CForm[currentTime]]]; s3D = 
 NDSolveValue[{eq2, ic, bcs}, p, {x, 0, 11}, {y, 0, 11}, {t, 0, 10}, 
  Method -> {"MethodOfLines"}, 
  EvaluationMonitor :> (currentTime = t;)];

But that gives errors about

which you'd need to fix.

edited Jun 16 '20 at 09:23

Community

1

answered Nov 06 '18 at 10:05

user21

39,710
8
110
167

score 2 · Accepted Answer · answered Nov 06 '18 at 12:57

I added boundary conditions and options to the solver. At large time t=10, the solution spoils, and at 0<t<1 it looks quite expected.

(*generate data*)
d = MultinormalDistribution[{1, 1}, {{2, -1/3}, {-1/3, 2/3}}];
data = Table[PDF[d, {x, y}], {x, -5, 5}, {y, -5, 5}];
dataintime = Table[data/(1.2^(t)), {t, 0, 10, 1}];
Animate[ListPlot3D[dataintime[[j]], 
  PlotRange -> {{1, 10}, {1, 10}, {0, 0.15}}], {j, 1, 10, 1}]
dataall = dataintime;
data = dataintime[[1]];


(*find fit*)
data3D = Flatten[MapIndexed[{#2[[1]], #2[[2]], #1} &, data, {2}], 1];
fm = NonlinearModelFit[
   data3D, (1/(2*Pi*sigx*sigy))*
    Exp[(-(((x - ux)^2)/(2*sigx^2) + ((y - uy)^2)/(2*sigy^2)))], {{ux,
      7}, {uy, 7}, {sigx}, {sigy}}, {x, y}];


(*put in coefficients*)
coeff1 = 2;
coeff2 = 2;
coeff3 = 2;

(*this equation will work as it has been linearised \
eq1=Derivative[0,0,1][p][x,y,t]\[Equal]coeff1*Laplacian[p[x,y,t],{x,y}\
]-coeff2*p[x,y,t];*)

(*equation to solve*)
eq2 = Derivative[0, 0, 1][p][x, y, t] == 
   coeff1*Laplacian[p[x, y, t], {x, y}] - coeff2*p[x, y, t] - 
    coeff3*p[x, y, t]^2;

(*initial conditions*)
ic = {p[x, y, 0] == fm[x, y]};

(*boundary conditions*)

bcs = {p[0, y, t] == fm[0, y], p[11, y, t] == fm[11, y], 
   p[x, 0, t] == fm[x, 0], p[x, 11, t] == fm[x, 11]};

s3D = NDSolveValue[{eq2, ic, bcs}, 
   p, {x, 0, 11}, {y, 0, 11}, {t, 0, 10}, 
   Method -> {"MethodOfLines", 
     "SpatialDiscretization" -> {"TensorProductGrid", 
       "MinPoints" -> 40, "MaxPoints" -> 100, 
       "DifferenceOrder" -> "Pseudospectral"}}, MaxSteps -> 10^6];
L = ListAnimate[
  Table[Plot3D[s3D[x, y, t], {x, 0, 11}, {y, 0, 11}, Mesh -> None, 
    PlotRange -> {0, .15}], {t, 0, 1, .025}], ControlPlacement -> Top]

Solving non-linear PDEs

2 Answers2