I am numerically solving the following ODE initially using NDSolve in Mathematica(updated and corrected):
$-(-\frac{z'(r)}{r \sqrt{z'(r)^2+1}}-\frac{z''(r)}{\left(z'(r)^2+1\right)^{3/2}})=A_1(z(r)+H)+A_2(\frac{A_3}{\sqrt{z(r)^2+r^2}-1})^3$
subject to boundary conditions of $z'(0) = 0$, and $z(\infty) = - H$. In this case, $r = 4$ or even 1 can be treated as infinity.
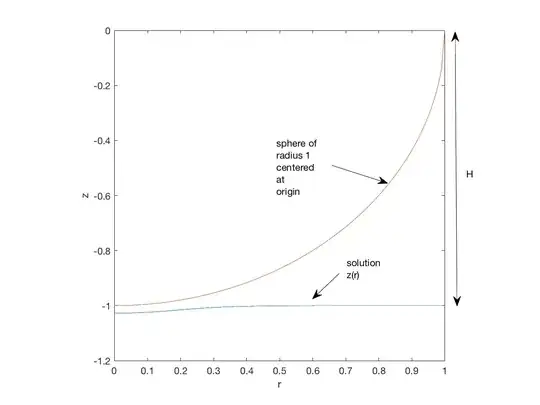
The left-hand-side is twice the mean curvature of a surface of revolution characterized by $z(r)$ in cylindrical coordinates. Parameters $A_1, A_2, A_3$ and $H$ are provided. I anticipated a solution that looked like this:
The expected solution (blue curve) is perturbed by the presence of the sphere near $r = 0$ and resumes its unperturbed shape (a straight line) at $r = \infty$. Note that H is the vertical distance of z(r) to the line of $z = 0$ at $r = \infty$..
The Mathematica code used:
A1 = 200;
A2 = 1.86*10^7;
A3 = 0.0002;
H=1;
f[z_, r_] := A1 (z + H) + A2 (A3/(Sqrt[z^2 + r^2]-1))^3;
k := -(z''[r]/(z'[r]^2 + 1)^(3/2)) - If[r == 0, 0, z'[r]/(r Sqrt[z'[r]^2 +1])]);
sol = NDSolve[{-k == f[z[r], r], z'[0] == 0, z[1] == -H}, z, {r, 0, 1}];
However, NDSolve was not able to yield sensible results, with $z(r)$ either blowing up to $z = \infty$ or simply "encountered stiffness", even if variations of the boundary conditions were attempted, i.e.
1) z'[0.0001] = 0, z[0.0001] = -1.01
2) z'[1] = 0, z[1] = - H
3) z'[0.0001 = 0, z[1] = -H
To my surprise, Matlab on the other hand handled the identical system well using bvp4c (4th order RK method) without blow-up, and yielded the solution shown in the figure above.
Any clue as to why Mathematica resulted in a blow-up solution yet Matlab converged well? Any explanations will be greatly appreciated.
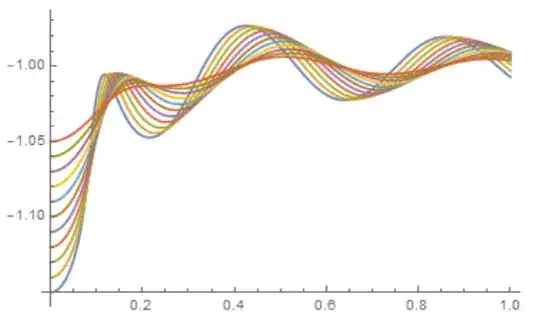
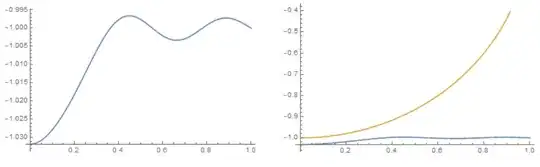

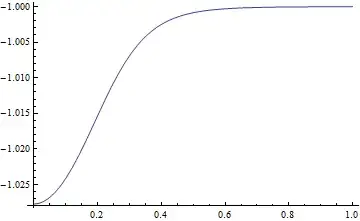
%% --- function dydx = twoode(x,y) A0=5.36e-14; Lambda=2.0e-10; G=1.0e4; R=1.0e-6; Tm=933; H=1e-6; A1=GR^2/A0/Tm; A2=GHR/A0/Tm; A3=R/A0; A4=Lambda/R; % A1=0; % A2=0; % A3=0; % A4=0; zpp=(A1y(1)+A2+A3(A4/(sqrt(y(1)^2+x^2)-1))^3)(1+y(2)^2)^1.5-y(2)*(1+y(2)^2)/x; %zpp=-abs(y(1)); dydx = [ y(2) zpp ]; end
– Linmin Nov 08 '18 at 21:17