Making StreamPlot draw phase plane streams near saddle points

Question

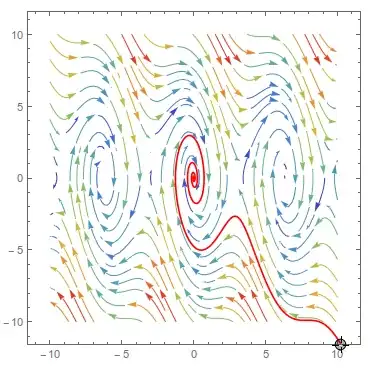
For example, I want to draw the phase portraits near the saddle points $(-\pi,0)$ and $(\pi,0)$, but the code that follows can not plot traces near those points, because $(y,\,-10 \sin x - y) = (0,\,0) at those points.

Evaluating

splot = 
  StreamPlot[{y, -10 Sin[x] - y}, {x, -10, 10}, {y, -10, 10}, 
  StreamColorFunction -> "Rainbow", StreamScale -> 0.12];

produces

How can I plot a phase portraits like this image (picture come from Halil, Nonlinear Systems, 3rd, Chapter 2). You can see vector field crossing the saddle points!

Possible duplicate of How to plot the stable and unstable manifolds of a hyperbolic fixed point of a nonlinear system of differential equations? — Chris K, Nov 09 '18 at 00:38

score 1 · Accepted Answer · answered Nov 09 '18 at 14:14

Code follows

Eq1 = x'[t] == y[t];
Eq2 = y'[t] == -10 Sin[x[t]] - y[t];
pendulum = 
  StreamPlot[{y, -10 Sin[x] - y}, {x, -10, 10}, {y, -10, 10}, 
   StreamScale -> 0.12];
man1 = Manipulate[Show[pendulum,
   ParametricPlot[
    Evaluate[
     First[{x[t], y[t]} /. 
       NDSolve[{Eq1, Eq2, Thread[{x[0], y[0]} == {-3.14, 0}]}, {x, 
         y}, {t, 1, 10}]]], {t, 1, 10}, PlotStyle -> Green],
   ParametricPlot[
    Evaluate[
     First[{x[t], y[t]} /. 
       NDSolve[{Eq1, Eq2, Thread[{x[0], y[0]} == {-3.15, 0}]}, {x, 
         y}, {t, 1, 10}]]], {t, 1, 10}, PlotStyle -> Purple], 
   ParametricPlot[
    Evaluate[
     First[{x[t], y[t]} /. 
       NDSolve[{Eq1, Eq2, Thread[{x[0], y[0]} == point]}, {x, y}, {t, 
         0, T}]]], {t, 0, T}, PlotStyle -> Red]], {{T, 0.1}, 0.1, 
   10}, {{point, {Pi, 2 Pi}}, Locator}, SaveDefinitions -> True]

Thanks for Chris's comment,Reference from How to plot the stable and unstable manifolds of a hyperbolic fixed point of a nonlinear system of differential equations?

This is still not showing the separatrices. – murray Nov 09 '18 at 15:22 — murray, Nov 09 '18 at 15:22

Making StreamPlot draw phase plane streams near saddle points

1 Answers1