I have just started using Mathematica. I want to solve a differential equation numerically with NDSolve. I have to specify an "initial condition" at -Infinity (note that the parameter t goes from -Infinity to 0) but I don't know how to do that. I've tried as shown below, but it gives me the following error: "Cannot find starting value for the variable y".
Thanks in advance!
eq = NDSolve [{y''[t] + (k^2 - 2/t^2) y[t] == 0,
y[-Infinity] == 1/Sqrt[2 k], y'[-Infinity] == -ik/Sqrt[2 k]},
y, {t, -100, 0} ]
I know that this equation has an analytical solution, but I would like to solve it with NDSolve in order to be able to apply this method where there are not.

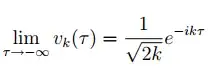
DSolve[y''[t] + (k^2 - 2/t^2) y[t] == 0, y[t], {t, -Infinity, 0}]resulting iny(t)->(I Sqrt[2/\[Pi]] ((Subscript[c, 2] k t-Subscript[c, 1]) sin(k t)+(Subscript[c, 1] k t+Subscript[c, 2]) cos(k t)))/((-k)^(3/2) t). Could you continue from here by bringing your boundary conditions into a similar form and dermining your unknown coefficients then? – gothicVI Nov 13 '18 at 15:32