I try to use Mathematica to evaluate:
$$\frac{\partial}{\partial A_{abc}} \sum_{j=1}^{J}\sum_{k=1}^{K}\log\left(\sum_{l=1}^{L}A_{jkl}B_{jkl}\right)$$
I get:
$$\sum_{j=1}^J \sum_{k=1}^K \frac{\begin{array}&\begin{cases} B(j,k,c) & a-j=0\land b-k=0 \\ 0 & \text{True} \\ \end{cases} \\ \end{array}}{\sum_{l=1}^L A(j,k,l) B(j,k,l)}$$
Instead of
$$\frac{B_{abc}}{\sum _{l=1}^L A_{abl} B_{abl}}$$
How to make Mathematica simplify the sum of conditional functions?
Alternatively, how to avoid the conditional functions in the first place?
The expression is part of a non-linear objective function containing multiple matrices. I am trying to evaluate the gradient and Hessian.
Thanks.
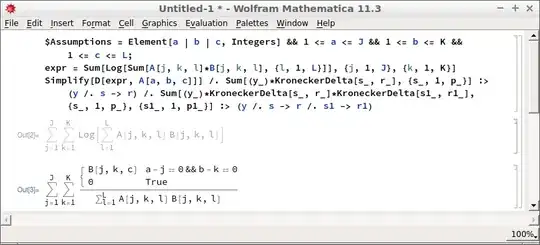
$Assumptions =
Element[a | b | c, Integers] && 1 <= a <= J && 1 <= b <= K &&
1 <= c <= L;
expr = Sum[
Log[Sum[A[j, k, l]*B[j, k, l], {l, 1, L}]], {j, 1, J}, {k, 1, K}]
Simplify[D[expr, A[a, b, c]]]
Update:
Try to simplify Kronecker delta with rules, as suggested by chris.
Simplify[D[expr, A[a, b, c]]]/. Sum[y_ KroneckerDelta[s_, r_],
{s_, 1, p_}] :> (y /. s -> r) /. Sum[y_ KroneckerDelta[s_, r_]
KroneckerDelta[s1_, r1_], {s_, 1, p_}, {s1_, 1, p1_}
] :> (y /. s -> r /. s1 -> r1)
Unfortunately, Mathematica doesn't even give Kronecker delta in this case.


Simplify[D[expr, A[a, b, c]]](* 0*) !!! Time for an update... – Ulrich Neumann Nov 20 '18 at 16:02