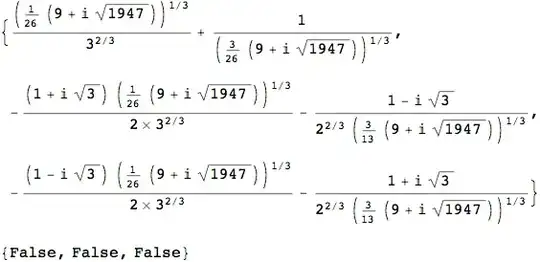How to check if an expression is a real-valued number

Question

What is a simple, fast way to test whether an expression is a real-valued number? I ask since there is no RealQ function.

If we call this test realQ, it should satisfy these constraints:

realQ["text"] is False (non numerics are all false)
realQ[0] is True (integers are true)
realQ[3.0] is True (reals are true)
realQ[1/2] is True (rationals are true)
realQ[I] is False (anything with an imaginary component is false)

Background: I thought of this as I was writing code to validate xmin or xmax for Plot[f[x],{,xmin,xmax}] in a web form. Even though I could write something, I thought there's probably more than one way to skin this cat, and it would make a good question for this site. You guys did not disappoint! — Joel Klein, Jan 29 '13 at 14:37

kglr · Accepted Answer · 2013-01-29T09:16:53.617

Update:

 Internal`RealValuedNumericQ /@ {1, N[Pi], 1/2, Sin[1.], Pi, 3/4, aa,  I}
 (* {True, True, True, True, True, True, False, False} *)

or

 Internal`RealValuedNumberQ /@ {1, N[Pi], 1/2, Sin[1.], Pi, 3/4, aa, I}
 (* {True, True, True, True, False, True, False, False} *)

Using @RM's test list

 listRM = With[{n = 10^5},
  RandomSample[Flatten[{RandomChoice[CharacterRange["A", "z"], n],
  RandomInteger[100, n],
  RandomReal[1, n],
  RandomComplex[1, n],
  RandomInteger[100, n]/RandomInteger[{1, 100}, n],
  Unevaluated@Pause@5}], 5 n + 1]];

and his realQ

 ClearAll@realQrm
 SetAttributes[realQrm, Listable] 
 realQrm[_Real | _Integer | _Rational] := True 
 realQrm[_] := False

timings

 realQrm@listRM; // AbsoluteTiming
 (* {0.458046, Null}  *)

 Internal`RealValuedNumericQ /@ listRM; // AbsoluteTiming
 (* {0.247025, Null} *)

 Internal`RealValuedNumberQ /@ listRM; // AbsoluteTiming
 (* {0.231023, Null} *)

 realQ = NumberQ[#] && ! MatchQ[#, _Complex] &
 realQ /@ {1, N[Pi], 1/2, Sin[1.], 3/4, aa, I}
 (* {True, True, True, True, True, False, False} *)

or

realQ2 = NumericQ[#] && ! MatchQ[#, _Complex] &
realQ3 = NumericQ[#] && FreeQ[#, _Complex] &

This is pretty close to what I started with, although I put everything into a single MatchQ. — Joel Klein, Jan 28 '13 at 23:44
Accepting, since this fulfills my original request for simple and fast. It was hard to decide, what we have now are all very good answers. — Joel Klein, Feb 01 '13 at 18:19

Mark McClure · Answer 2 · 2013-01-29T14:42:54.723

As the responses show, there are a number of quick "probably real" tests. In general, the problem is undecidable, however. This is an easy corollary of Richardson's theorem, which says that it is impossible to decide if two real expressions $x$ and $y$ are equal. Assuming Richardson's theorem, note that $(x-y)i$ is real if and only if $x=y$.

As a more mundane example, that arises in common practice with Mathematica, consider the polynomial $p(x)=13x^3-13x-1$. It's easy to see that all three roots are real (even if they don't look it), yet they don't pass any of the test here.

roots = x /. Solve[13 x^3 - 13 x - 1 == 0, x]
Internal`RealValuedNumericQ /@ roots

enter image description here

score 20 · Answer 3 · answered Jan 28 '13 at 23:36

20

RealQ[x_] := Element[x, Reals] === True

It fulfills all your samples and I think is generally correct.

answered Jan 28 '13 at 23:36

0xFE

1,038
7
19

1

This is probably the most readable so far. – Joel Klein Jan 28 '13 at 23:43
11

TrueQ@Element[x, Reals] – Rojo Jan 29 '13 at 00:50
2

In case it's not clear -- this proposed test, too, fails with Mark McClure's example of the roots of $13x^3-13x-1$. – murray Sep 10 '13 at 15:10
1

Why do you compare the result of Element[...] to True? – Qbyte Mar 26 '20 at 16:25

rm -rf · Answer 4 · 2013-01-29T14:37:04.797

15

I think a solution based on pattern matching will be much faster than using Element (which is more mathematical in nature) or only pattern tests or anything else that forces evaluation, since we can bypass the main evaluator. However, it is not possible to completely escape evaluation, because there can be infinitely large number of possibilities for a real number that cannot be matched solely by pattern matching. Hence, the following tries to delegate as much as possible to the pattern matcher and evaluates only what's necessary. The unfortunate consequence is that it is no longer immune to prank entries such as Unevaluated@Pause@10.

ClearAll@realQ
SetAttributes[realQ, Listable]
realQ[_Real | _Integer | _Rational] := True

realQ[Catalan | ChampernowneNumber | Degree | E | EulerGamma | Internal`Euler2Gamma |
      Glaisher | GoldenRatio | Khinchin | MachinePrecision | Pi] := True

realQ[Complex[_, 0.]] := True
realQ[x_] := NumericQ[x]

realQ[{"text", 0, 3.0, 1/2, I, Pi, 1 + 0. I}]
(* {False, True, True, True, False, True, True} *)

The list in the second definition was obtained using

Select[Names["*`*"], MemberQ[Attributes@#, Constant] &]

edited Jan 29 '13 at 14:37

answered Jan 28 '13 at 23:39

rm -rf

88,781
21
293
472

Pretty direct translation of the spec I gave, and listable to boot. I wish it didn't have the 3 alternatives of Real, Integer, and Rational though, I kind of like starting with the knowledge that we have a numeric (eliminate strings and such) and then exclude complex. – Joel Klein Jan 28 '13 at 23:46
@Joel You mentioned expression generally and wanted it to also be fast & simple and I think this satisfies both. This is faster than the others and also doesn't evaluate anything. For example, compare the speeds with list = With[{n = 10^5}, RandomSample[ Flatten[{RandomChoice[CharacterRange["A", "z"], n], RandomInteger[100, n], RandomReal[1, n], RandomComplex[1, n], RandomInteger[100, n]/RandomInteger[{1, 100}, n], Unevaluated@Pause@5}], 5 n + 1]];. Evaluation in the other solutions makes their timing on the order of 5s, compared to 0.3s for mine (on my machine). – rm -rf Jan 28 '13 at 23:56
Good explanation. – Joel Klein Jan 29 '13 at 02:27
What about Pi? – Mark McClure Jan 29 '13 at 12:24
You can add realQ[c_Complex] := PossibleZeroQ[Im[c]] if you want 0.I etc to be real – ssch Jan 29 '13 at 13:29
@MarkMcClure and ssch: Thanks, added condition for Pi and zero imaginary part complex numbers. It still doesn't evaluate except for symbols. – rm -rf Jan 29 '13 at 14:13
And I guess you are "often" avoiding evaluation, but not always. – Mark McClure Jan 29 '13 at 14:22
@MarkMcClure Sadly, that seems to be the case. I don't think any robust solution can be 100% free of evaluation, as cases like Sin[1] or Pi + E, etc. will never be found and the possibilities are too large (perhaps impossible) to handle via pattern matching alone. So what I've done is to push as much as possible to the pattern matcher and evaluate only what's left. However, it looks like kguler's find is the best option. – rm -rf Jan 29 '13 at 14:39
Hmm... I'm suddenly feeling queasy about 0.0I being real. Note that InternalRealValuedNumberQ[0.0I]returnsFalse`. – Mark McClure Jan 29 '13 at 14:41
@MarkMcClure One could say it depends on the use case, and it's just a definition that can be added/taken out. – rm -rf Jan 29 '13 at 14:42

score 7 · Answer 5 · answered Jan 29 '13 at 14:51

7

I wasn't planning to add an answer, but this now seems like it has its place in this fine list of answers:

realQ[x_?NumericQ] := Head[x] =!= Complex
realQ[_] := False

While maybe not the absolute fastest, it is fast and also relatively simple and uses only System` functions.

answered Jan 29 '13 at 14:51

Joel Klein

5,225
1
31
44

1

This works only until quaternions are not properly integrated into Mathematica :) – István Zachar Sep 10 '13 at 12:54

eldo · Answer 6 · 2023-09-19T08:15:38.700

5

Since V 13.3 we have RealValuedNumberQ and RealValuedNumericQ

col[dt_, f_] := ToString[f] -> AssociationThread[Map[HoldForm, dt] -> Map[f, dt]]
head[dt_] := "Head" -> AssociationThread[Map[HoldForm, dt] -> Map[Head, dt]]
test = {Pi, x[1], "text", 0, 3.0, 1/2, I, 1 + 0. I}
<|head[test], col[test, RealValuedNumberQ], 
   col[test, RealValuedNumericQ]|> // Transpose // Dataset

edited Sep 19 '23 at 08:15

answered Sep 19 '23 at 07:47

eldo

67,911
5
60
168

score 1 · Answer 7 · answered Apr 27 '16 at 14:52

1

Surely the simplest way to do this is just to check whether the imaginary part is zero:

Im[z] == 0

This will return true if z is a real number and false if z is complex.

answered Apr 27 '16 at 14:52

Gabriel Hawkins-Pottier

11
1

3

Try it on the OP's first example Im["text"] == 0. You might want to consider Mark McClure's example, too. – Michael E2 Apr 27 '16 at 15:13

How to check if an expression is a real-valued number

7 Answers7

Linked

Related