Subdivision of a line into n intervals of linearly changing length

Question

This question is separate, but connected to my previous question on this site, that can be found here.

Let's say that we have a line of length X (in this case X=5), defined by a list

LineList={{0,0},{5,5}}

I would like to divide this line into an arbitrary number of subdivisions, that change in length linearly from one end to the other. I would also like to be able to arbitrarily define the ratio of

ratio=(LongestDivision)/(ShortestDivision)>=1

So for the simple case of n=2 and ratio=2, you would obtain a list

NewLineList={{0,0},{10/3,10/3},{5,5}}

Is is possible to apply such an algorithm to an arbitrary parametric curve?

Any help is much appreciated.

EDIT: It seem that my question was poorly written, so just to clarify, I wish the number of divisions to be independent of the ratio. An example of this would be

n=4, ratio=10, which would result in a line divided to 4 subintervals, with their lengths as

L1:L2:L3:L4=1:3.33:6.67:10.

For a case of n=4, ratio=2, this would produce L1:L2:L3:L4=1:1.33:1.67:2.

Related: https://mathematica.stackexchange.com/questions/8454/generating-evenly-spaced-points-on-a-curve/ — Michael E2, Nov 22 '18 at 16:08

Michael E2 · Answer 1 · 2018-11-23T18:45:26.893

Is is possible to apply such an algorithm to an arbitrary parametric curve?

Here's a way to plot them:

div = #/Last@# &@ Accumulate@ Range[0, 50];
plot = ParametricPlot[{t Cos[4 t], t Sin[5 t]}, {t, 0, 2 Pi}, 
  MeshFunctions -> {"ArcLength"}, Mesh -> {div}, MeshStyle -> Red]

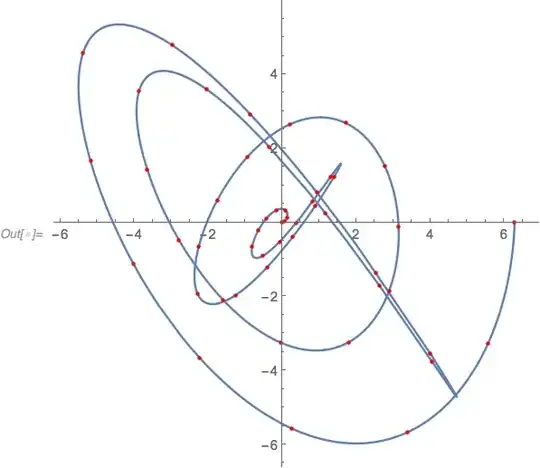
One can get the points with the following; but plotting is not a very accurate solver and the mesh points are generated out of order:

pts = Cases[Normal@plot, Point[p_] :> p, Infinity]

For a nonsingular parametrization, one can integrate the parameter t as a function of arclength. Then one can get accurate values for the points in order:

param = {t Cos[4 t], t Sin[5 t]};
tdom = {0, 2 Pi};
tIF = NDSolveValue[{
    t'[s] == 1/Sqrt[#.#] &[D[param, t] /. t -> t[s]],
    t[0] == First@tdom,
    WhenEvent[t[s] == Last@tdom, "StopIntegration"]},
   t, {s, 0, Infinity}];

pts = param /. t -> tIF@Rescale[div, {0, 1}, First@tIF@"Domain"] // Transpose;

Show[
 plot,
 Graphics[{Orange, PointSize@Large, Point@%}]
 ]

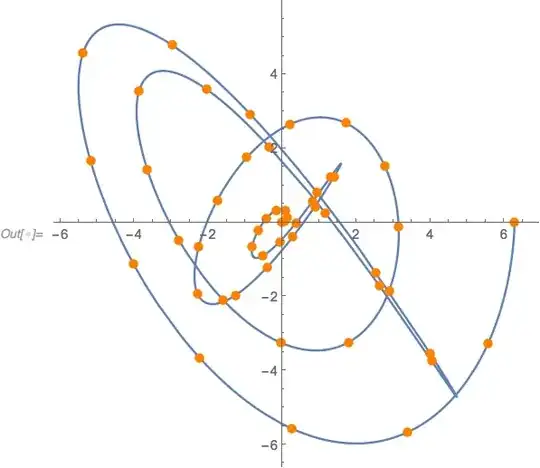
Response to updated Q (as well as some of the comments): The OP seems particularly interested in a general way to subdivide an interval {a, b} such the lengths of the divisions are in an arithmetic progression specified by the number of subintervals and the ratio of the longest and shortest lengths (the first and last lengths). One can work out a formula with HS algebra, but one could also leave the work to Rescale as above. One can start from an arithmetic sequence of lengths from 1 to the ratio and generate the subdivision from there:

Subdivide[1, r, n - 1] //        (* arithmetic sequence of lengths *)
   Prepend[0] //                 (* prepend zero so Accumulate includes endpoint *)
  Accumulate //                  (* relative divisions *)
 Rescale[#, MinMax@#, {a, b}] &  (* rescale to interval {a, b} *)

Compare with div and rescaling it to get the second pts above.

Here's a function that has a few bells & whistles: It computes either increasing or decreasing lengths; it maintains the precision of the input; it produces a packed array when the input precision is MachinePrecision.

ClearAll[withWP];
SetAttributes[withWP, HoldRest];
withWP[wp_, code_] :=        (* set up environment for a fixed working precision *)
  Block[{$MinPrecision = wp, $MaxPrecision = wp}, code];

ClearAll[divisions];
divisions[{a_, b_}, r_?(GreaterEqualThan[1]), n_Integer?(GreaterThan[1])] :=  
  withWP[Precision[{a, b, r}],          (* working precision determined by input *)
   Subdivide[N[1, $MaxPrecision], r, n - 1] // (* arithmetic sequence of lengths *)
   Prepend[N[0, $MaxPrecision]] //      (* prepend zero to include endpoint *)
      Accumulate //                         (* relative divisions *)     
     Rescale[#, MinMax@#, {a, b}] & //      (* rescale to interval {a, b} *)
        If[TrueQ[a > b], Reverse, Identity] (* decreasing div. lengths if a > b *)
   ];

Examples of divisions[interval, ratio, n]:

divisions[{a, b}, 2, 2]             (* symbolic subdivision *)
(*  {a, a + 1/3 (-a + b), b}  *)

divisions[{5, 0}, 2, 2]             (* decreasing lengths *)
(*  {0, 10/3, 5}  *)

divisions[{2., 9.}, 2, 4]           (* increasing lengths *)
Ratios@ MinMax@ Differences@ %
#/Min[#] &@ Differences@ %%
(*
  {2., 3.16667, 4.72222, 6.66667, 9.}
  {2.}                                 ratio = 2
  {1., 1.33333, 1.66667, 2.}           OP's L1:L2:L3:L4
*)

divisions[{2., 9.}, 2, 4] // Developer`PackedArrayQ
(*  True  *)

#/Min[#] &@ Differences@ divisions[{2., 9.}, 10, 4]
(*  {1., 4., 7., 10.}  ratio of lengths...
      OP gets L1:L2:L3:L4=1:3.33:6.67:10 but I think this is correct *)

If you do the algebra, you can shorten divisions:

divisions2[{a_, b_}, r_?(GreaterEqualThan[1]), n_Integer?(GreaterThan[1])] :=
  withWP[Precision[{a, b, r}],          (* working precision determined by input *)
   ((n - 1)/(r - 1) - 1/2 + Range[N[0, $MaxPrecision], N[n, $MaxPrecision]])^2 //
         Rescale[#, MinMax@#, {a, b}] & //   (* rescale to interval {a, b} *)
    If[TrueQ[a > b], Reverse, Identity]      (* decreasing div. lengths if a > b *)
   ];

Ulrich Neumann · Accepted Answer · 2018-11-23T09:25:51.247

3

The case ratio!=n with linear increasing gridsize leads to list of gridpoints

x[n_, ratio_] := Accumulate[ Join[{0}, Table[1 + (i - 1)/(n - 1) (ratio - 1), {i, 1, n}]]]  (*//Normalize*)

which gives (without normalization...)

x[2,4] (*{0, 1, 5}*)
x[3,4](*{0, 1, 11/4, 21/4, 17/2, 25/2}*)
%//Differences
(*{1, 7/4, 5/2, 13/4, 4}*)

edited Nov 23 '18 at 09:25

answered Nov 22 '18 at 16:01

Ulrich Neumann

53,729
2
23
55

While this algorithm does the job for a case where n=ratio, I would like to have a more general one, where the ratio of the longest section to the shortest section and the number of divisionsn are not the same. So that on an interval of [0,1], using n=2 and ratio=4, I would get {0,4/5,1}. For n=2 the algorithm is quite simple, but for more than 2 division, I do not know how to handle this. – Marko Nov 23 '18 at 07:41
So for n=3 and q=4 you would expect {0,16,20,21}/21? – Ulrich Neumann Nov 23 '18 at 08:07
For n=3 and q=4, I would expect {0,1,3,7}/7, making it so that the last division is of length 4, the first is of length 1 and all the middle ones are just linearly increasing. So for n=5 and q=4, it would go {0,1,11/4,21/4,24/4,40/4}/(40/4) – Marko Nov 23 '18 at 08:25
Until now the intervalls were decreasing... – Ulrich Neumann Nov 23 '18 at 08:28
As for the intervals increasing or decreasing, I don't have a preference. Both versions would be great. – Marko Nov 23 '18 at 08:31
Your example n=5,q=4seems to be wrong: {0, 1, 11/4, 21/4, 24/4, 40/4}/(40/4) // Differences // N evaluates to nonmonotonic intervalls {0.1, 0.175, 0.25, 0.075, 0.4} – Ulrich Neumann Nov 23 '18 at 08:33
You are correct. The correct solution should be: {0,1,11/4,21/4,34/4,50/4}/(50/4). This would then produce the effect that I wish. – Marko Nov 23 '18 at 08:41
My answer is edited ... – Ulrich Neumann Nov 23 '18 at 09:26

kglr · Answer 3 · 2018-11-22T16:37:54.100

ClearAll[subDivide]
subDivide = Rationalize[BSplineFunction[#] /@ 
   Normalize[Accumulate@RotateRight@Reverse@Range[0, #2], Max]] &;

subDivide[LineList, 2]

{{0, 0}, {10/3, 10/3}, {5, 5}}

subDivide[LineList, 3]

{{0, 0}, {5/2, 5/2}, {25/6, 25/6}, {5, 5}}

subDivide[{0, 1}, 10]

{0, 2/11, 19/55, 27/55, 34/55, 8/11, 9/11, 49/55, 52/55, 54/55, 1}

Total[Range@10] Differences @ subDivide[{0, 1}, 10]

{10, 9, 8, 7, 6, 5, 4, 3, 2, 1}

ZaMoC · Answer 4 · 2018-11-23T10:19:00.037

1

Can you try this one?

n = 2;
LineList = {{0, 0}, {5, 5}}
x1 = LineList[[2]]
x2 = LineList[[1]]
x = Reverse@FoldList[# + 1/(n*(n + 1)/2)*#2 (x2 - x1) &, x1, Range@n]

{{0, 0}, {10/3, 10/3}, {5, 5}}

here is an example for

n = 10
LineList[{{0, 6}, {5, 25}}]

EDIT

Here is the function you are asking for increasing intervals in [0,1]

F[n_, r_] := Accumulate@Join[{0}, Table[i*t + d, {i, 0, n - 1}]] /. 
Solve[((n - 1) t + d)/d == r && n*d + (n - 1) n/2 t == 1, {t, d}]

for example for n=5 and r=4 we get

F[5,4]

{{0, 2/25, 11/50, 21/50, 17/25, 1}}

which matches your example

edited Nov 23 '18 at 10:19

answered Nov 22 '18 at 15:55

ZaMoC

6,697
11
31

While this algorithm does the job for a case where n=ratio, I would like to have a more general one, where the ratio of the longest section to the shortest section and the number of divisionsn are not the same. So that on an interval of [0,1], using n=2 and ratio=4, I would get {0,4/5,1}. For n=2 the algorithm is quite simple, but for more than 2 division, I do not know how to handle this. – Marko Nov 23 '18 at 07:51

Subdivision of a line into n intervals of linearly changing length

4 Answers4