Finding position at given distance in a GeoPath

Question

Is there a way to find the geoposition of a given distance from start in a GeoPath? I want to mark equidistant positions along a track, for example, a mark every 500 km along the path given by

path=GeoGraphics[
  GeoPath[{
    Entity["City", {"Boston", "Massachusetts", "UnitedStates"}],
    Entity["City", {"Rochester", "NewYork", "UnitedStates"}], 
    Entity["City", {"Chicago", "Illinois", "UnitedStates"}]
  }, "Rhumb"]
]

Is there a way to find the pos that gives GeoDistance[Entity["City", {"Boston", "Massachusetts", "UnitedStates"}],pos]==500 km along the path?

Answer 1

Here's my attempt to parametrize the path by arclength, where here arclength is GeoLength.

First I build up a function that can be used on many values:

ParametrizeGeoPath[g_GeoPath, t_] := ParametrizeGeoPath[g][t]

ParametrizeGeoPath[GeoPath[locs_, args___]] :=
  Block[{line, nodes, lens, acc, nf, n1, n2, solver},
    line = GeoGraphics`GeoEvaluate[GeoPath[locs, args]];
    nodes = GeoPosition /@ Reverse[line[[1]], {2}];
    lens = QuantityMagnitude[UnitConvert[GeoLength[GeoPath[#, args]]& /@ Partition[nodes, 2, 1], "Kilometers"]];
    acc = Accumulate[lens];
    nf = Nearest[acc -> {"Index", "Element"}];

    GeoPathParametricFunction[acc, nodes, nf, args]
  ]

Given a target distance, we can invert GeoLength with FindRoot:

GeoPathParametricFunction[_, nodes_, __][d_] /; d == 0 := First[nodes]

GeoPathParametricFunction[acc_, nodes_, __][d_] /; d == Last[acc] := Last[nodes]

GeoPathParametricFunction[acc_, nodes_, nf_, args___][d_] /; 0 < d < Last[acc] :=
  Block[{i, v, s, n1, n2, dist, root, t = Unique["t"]},
    {i, v} = First[nf[d]];
    If[v > d, i--];
    s = If[i == 0, 0, acc[[i]]];
    n1 = nodes[[i+1, 1]];
    n2 = nodes[[i+2, 1]];

    dist[t_?NumericQ] := s + QuantityMagnitude[UnitConvert[GeoLength[GeoPath[{GeoPosition[n1], GeoPosition[(1-t)n1 + t n2]}, args]], "Kilometers"]];

    root = Quiet@FindRoot[dist[t] == d, {t, .5, 0, 1}];

    (
      GeoPosition[(1-t)n1 + t n2] /. root

    ) /; MatchQ[root, {t -> _Real}]
  ]

GeoPathParametricFunction[___][d_?NumericQ] = Indeterminate;

GeoPathParametricFunction /: MakeBoxes[expr:GeoPathParametricFunction[__], _] := InterpretationBox[RowBox[{"GeoPathParametricFunction", "[", "\"\[Ellipsis]\"", "]"}], expr]

Your example:

path = GeoPath[{
  Entity["City", {"Boston", "Massachusetts", "UnitedStates"}],
  Entity["City", {"Rochester", "NewYork", "UnitedStates"}], 
  Entity["City", {"Chicago", "Illinois", "UnitedStates"}]
}, "Rhumb"];

gpf = ParametrizeGeoPath[path];

gpf[500]

 GeoPosition[{43.0932, -77.0359}]

Manipulate[GeoGraphics[{
    path,
    GeoMarker[gpf[d]]
  }, 
  PlotLabel -> Row[{"Distance: ", Quantity[d, "Kilometers"]}]], 
  {d, 0, gpf[[1, -1]]}
]

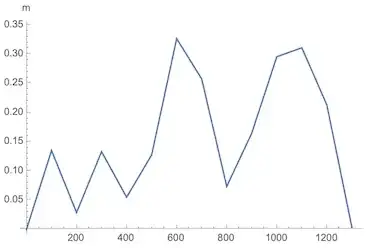
The points returned are very close to the initial path:

ListLinePlot[
  GeoDistance[path, g /@ Range[0, 1300, 100]], 
  TargetUnits -> "Meters", 
  AxesLabel -> Automatic, 
  DataRange -> {0, 1300}
]

Answer 2

Here is a function for finding GeoPositions between 2 cities with certain step

city1 = Entity["City", {"Boston", "Massachusetts", "UnitedStates"}];
city2 = Entity["City", {"Rochester", "NewYork", "UnitedStates"}];
city3 = Entity["City", {"Chicago", "Illinois", "UnitedStates"}];

geopath[c1_, c2_, step_] := Module[{s = First@GeoDistance[c1, c2],
a = GeoDirection[c1, c2]},
GeoPath[NestList[GeoDestination[#,{1000 step,a}]&,c1,Floor[s/step]],"Rhumb"]]

Now if you want to find positions from city1 to city2 every 100 km, type

geopath[city1, city2, 100]    

and you will get the positions

GeoPath[{Entity["City", {"Boston", "Massachusetts", "UnitedStates"}], GeoPosition[{42.5124, -72.2106}], GeoPosition[{42.6928, -73.4044}], GeoPosition[{42.8732, -74.6017}], GeoPosition[{43.0535, -75.8026}], GeoPosition[{43.2338, -77.0069}]}, "Rhumb"]