Minimize distance between two lists

Question

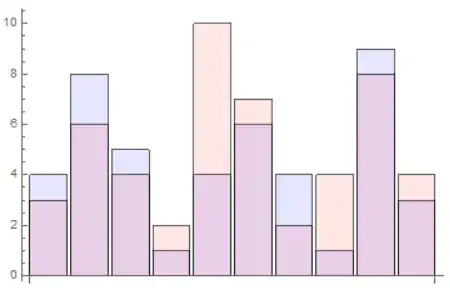
Writing:

expectedresults = {4, 8, 5, 1, 4, 6, 4, 1, 9, 3};
achievedresults = {3, 6, 4, 2, 10, 7, 2, 4, 8, 4};
p1 = BarChart[expectedresults, ChartStyle -> Directive[Opacity[0.1], Blue]];
p2 = BarChart[achievedresults, ChartStyle -> Directive[Opacity[0.1], Red]];
Show[p1, p2]

I get:

On the other hand, if I write:

k = 0.83;
expectedresults = {4, 8, 5, 1, 4, 6, 4, 1, 9, 3};
achievedresults = {3, 6, 4, 2, 10, 7, 2, 4, 8, 4} k;
p1 = BarChart[expectedresults, ChartStyle -> Directive[Opacity[0.1], Blue]];
p2 = BarChart[achievedresults, ChartStyle -> Directive[Opacity[0.1], Red]];
Show[p1, p2]

I get:

where it is clear that, compared to the previous case, in some bars the gap has decreased and in others it has increased.

Question: How can I determine the best value of k to get the smallest possible gap?

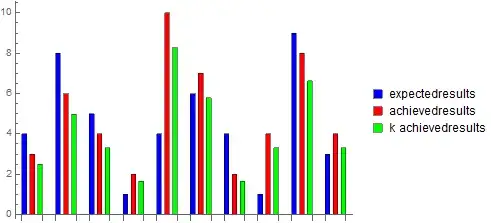
Writing:

h = -0.35;
k = 0.83;
expectedresults = {4, 8, 5, 1, 4, 6, 4, 1, 9, 3};
achievedresults = h + k {3, 6, 4, 2, 10, 7, 2, 4, 8, 4};
p1 = BarChart[expectedresults, ChartStyle -> Directive[Opacity[0.1], Blue]];
p2 = BarChart[achievedresults, ChartStyle -> Directive[Opacity[0.1], Red]];
Show[p1, p2]

I get:

Question 2: is it possible to determine the pair of values h, k that minimize the gap?

This is a related question: How to find the distance of two lists? — Artes, Nov 29 '18 at 16:03

Chris · Answer 1 · 2018-11-28T21:45:26.620

7

{k, h} = PseudoInverse[{#, 1} & /@ achievedresults].expectedresults

{35/64, 113/64}

edited Nov 28 '18 at 21:45

answered Nov 28 '18 at 20:36

Chris

1,076
5
9

2

Why do you add a zero column? I think PseudoInverse[Transpose[{achievedresults}]].expectedresults will do – MeMyselfI Nov 28 '18 at 20:56
1

@MeMyselfI Nice! Even better – Chris Nov 28 '18 at 21:05

kglr · Accepted Answer · 2018-11-28T21:52:05.753

Update: Using two parameters:

lmf2 = LinearModelFit[data, t, t];
Normal@lmf2

1.76563 + 0.546875 t

lmf2["BestFitParameters"]

{1.76563, 0.546875}

Fit[data, {1, t}, t]

1.76563 + 0.546875 t

ClearAll[h, k]
NMinimize[Total[Subtract[expectedresults, h + k achievedresults]^2], {h, k}]

{43.3594, {h -> 1.76562, k -> 0.546875}}

N @ LeastSquares[Thread[{1, achievedresults}], expectedresults]

{1.76563, 0.546875}

Original answer:

expectedresults = {4, 8, 5, 1, 4, 6, 4, 1, 9, 3};
achievedresults = {3, 6, 4, 2, 10, 7, 2, 4, 8, 4};
data = Transpose[{ achievedresults,expectedresults}];

You can use LinearModelFit or Fit or NMinimize or LeastSquares to get the value of k that minimizes the sum of squared distances between expectedresults and k achievedresults:

lmf = LinearModelFit[data, t, t, IncludeConstantBasis -> False]

Normal@lmf

0.828025 t

Normal @ LinearModelFit[{Transpose[{achievedresults}], expectedresults}]

0.828025 #1

Fit[data, {t}, t]

0.828025 t

ClearAll[k]
NMinimize[Total[Subtract[expectedresults, k achievedresults]^2], k]

{49.7134, {k -> 0.828025}}

N@LeastSquares[Thread[{achievedresults}], expectedresults]

{0.828025}

k = lmf["BestFitParameters"][[1]]

0.828025

p1 = BarChart[expectedresults, ChartStyle -> Directive[Opacity[0.1], Blue]];
p2 = BarChart[k achievedresults, ChartStyle -> Directive[Opacity[0.1], Red]];
Show[p1, p2]

BarChart[Transpose@{expectedresults, achievedresults,  k achievedresults}, 
 ChartStyle -> {Blue, Red, Green}, ChartLayout -> "Grouped", 
 ChartLegends -> {"expectedresults", "achievedresults", "k achievedresults"}]

For general data you can always find several values of $k$ that eliminate the difference between whichever bars you like. — David G. Stork, Nov 28 '18 at 20:42
@TeM, If you compare the NMinimize result adding the intercept parameter improves the squared loss from 49.7134 to 43.3594. — kglr, Nov 28 '18 at 21:54

Minimize distance between two lists

2 Answers2