I have an eigenvalue problem:
$$-\frac{d^2}{dx^2} \psi(x) +V(x)\psi(x) = E \psi(x)$$
where $V(x)$ is a complex periodic potential: $$V(x) = 4[\cos^2(x) + i 0.3 \sin(2x)]$$
It has been claimed that the eigenvalues of this problem are all real (this is always the case if the coefficient of $\sin$ is less than $0.5$, which in this case is $0.3$), although it's not Hermitian.
To verfy this, I have used the code provided here by @Jens periodic boundary conditions and NDEigensystem. But, Mathematica doesn't return anything.
The code in the above link is (with an additional 1/2 for the kinetic term):
spectrum[n_, dim_: 10000][potential_, {var_, varMin_, varMax_}, kBloch_: 0] :=
Module[
{e, v, vRange, dx, grid, potentialGrid, eKin, ePot, min, interpolate},
vRange = varMax - varMin;
interpolate =
ListInterpolation[Append[#, First[#]], {{varMin, varMax}},
PeriodicInterpolation -> True] &;
dx = N[vRange/dim];
grid = Range[varMin, varMax, dx];
eKin = -(1/2)
NDSolve`FiniteDifferenceDerivative[2, grid,
PeriodicInterpolation -> True]["DifferentiationMatrix"] -
I kBloch NDSolve`FiniteDifferenceDerivative[1, grid,
PeriodicInterpolation -> True]["DifferentiationMatrix"];
potentialGrid = Table[potential + kBloch^2/2, {var, Most[grid]}];
(* eKin is periodically interpolated,
so its last element is internally dropped by FiniteDifferenceDerivative, as redundant. Therefore,
I also have to drop the last grid element in potentialGrid. *)
min = Min[potentialGrid];
(* Matrix for the potential is shifted so its minimum entry is zero, guaranteeing that eigenvalues will be sorted in descending order: *)
ePot = DiagonalMatrix[SparseArray[potentialGrid - min]];
{e, v} = Eigensystem[eKin + ePot, -n];
(* Final step: turn vectors on spatial grid back into functions of x by interpolation: *)
Append[
Reverse /@ {e + min, Map[interpolate[#/Max[Abs[#]]] &, v]},
(* In the eigenvalues,
potential offset min was added back to get original energy scale. *)
interpolate[potentialGrid]
]]
And the potential is defined (with an extra 1/2):
potential[x_] = 1/2 (4((Cos[x])^2 + I 0.3 Sin[2x]));
{eigenvals, eigenvecs, pot} = spectrum[7][potential[x], {x, -Pi/2, Pi/2}];
2 eigenvals
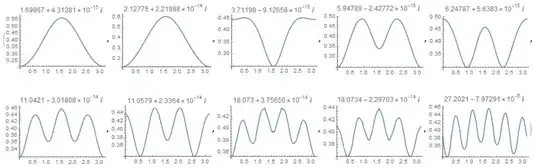

NDEigensystemfor this? – user21 Dec 02 '18 at 09:33