I have the following data points:
Clear["Global`*"]
dados={{0,0},{1,1000},{2,-750},{3,250},{4,-1000},{5,0}};
From these data I obtained the following interpolation:
Clear["Global`*"]
dados={{{0},0,0},{{1},1000,0},{{2},-750,0},{{3},250,0},{{4},-1000,0},{{5},0,0}};
Plot[Interpolation[dados][x],{x,0,5},ImageSize->500,Epilog->{Red,PointSize[0.01],Point@Partition[Flatten[dados],3][[All,1;;2]]}]
Is it possible to get the polynomial that describes this movement?
Or is it unlikely due to the derivatives at the inflection points?
As the Interpolation function used is it possible to "order" some polynomial?
EDIT
I added the InterpolatingPolynomial function, according to Szabolcs, but the function partially fulfilled what I wanted ...
Clear["Global`*"]
dados = {{{0}, 0, 0}, {{1}, 200, 0}, {{2}, -300, 0}, {{3}, 1000,
0}, {{4}, -800, 0}, {{5}, 0, 0}};
InterpolatingPolynomial[dados, t] // Simplify
Plot[%, {t, 0, 5}]

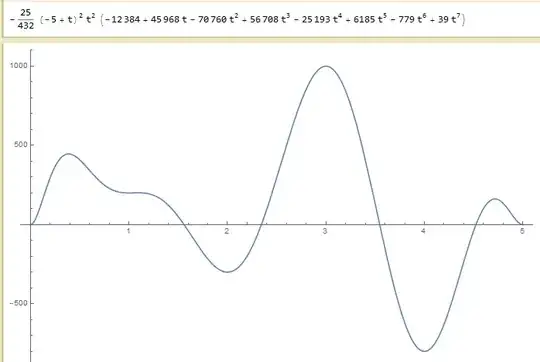
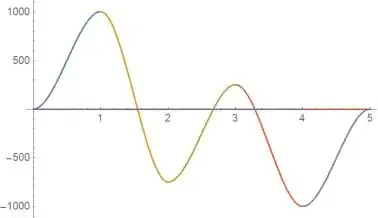


InterpolatingPolynomial? – Szabolcs Dec 03 '18 at 13:33InterpolatingPolynomialis among solutions provided for your last question. – Kuba Dec 03 '18 at 14:39