I'm trying to solve :
NSolve[3 r Sqrt[x/(1 - x)] + 1/2 r^3 (x/(1 - x))^(3/2) - (
3 r x Csch[r Sqrt[x/(1 - x)]])/(1 - x) == 0, {x, 0.5, 1}, {r, 0,
5}]
My goal is to have a relation r(x), with r in [0,5] and x in [0.5,1] But it looks like I'm not writing the command well because I'm getting the error:
NSolve: 0.5` is not a valid variable.
How I can achieve what I want plz ?
I've answered this type question before (for instance, here and here), as follows:
rFN = NDSolveValue[{3 r Sqrt[x/(1 - x)] +
1/2 r^3 (x/(1 - x))^(3/2) -
(3 r x Csch[r Sqrt[x/(1 - x)]])/(1 - x) == 0 /. r -> r[x],
t'[x] == 1, t[0.5] == 0.5}, r, {x, 0.5, 1}];
ListLinePlot@rFN
I ignore the error message at x == 1, which should be expected.
Of course if the function is not wanted and only a plot is desired, @Αλέξανδρος Ζεγγ has pointed out ContourPlot, which is easily found in the documentation.
NDSolve uses FindRoot to construct a table of values for r[x], which gets returned in an InterpolatingFunction. You need the t'[x] DE to trick it into constructing r[x]. Another approach would be to differentiate the equation and reintegrate with NDSolve. See for example, this.
– Michael E2
Dec 05 '18 at 15:26
Y = NDSolveValue[{x^2 + y[x]^2 == 1, Derivative[1][t][x] == 1, t[-1] == -1}, y, {x, -1, 1}], Plot[Y[u], {u, -1, 1}] but failed in finding the circle. What's wrong? Thanks.
– Ulrich Neumann
Dec 05 '18 at 16:15
y[x] is singular. Try Y = NDSolveValue[{x^2 + y[x]^2 == 1, t'[x] == 1, t[0] == 0}, y, {x, -1, 1}]
– Michael E2
Dec 06 '18 at 00:25
y'->Infinity?
– Ulrich Neumann
Dec 06 '18 at 08:37
y' -> Infinity. It's sometimes called a weak singularity. But it's probably better to think in terms of the inverse function theorem, so that when solving $F(x,y)=0$, $y'$ is undefined if $\partial F/\parital y = 0$. It's not necessary that $y' \rightarrow \infty$. For instance, the lemniscate NDSolveValue[{(x^2 + y[x]^2)^2 == x^2 - y[x]^2, t'[x] == 1, t[0] == 0}, y, {x, -1, 1}] fails. It also fails if the IC is at $x =\pm1$, but succeeds if integration is started sufficiently far from $-1, 0, 1$ but within $-1<x<1$.
– Michael E2
Dec 06 '18 at 11:38
As has been mentioned, one can get the curve by ContourPlot
f[x_, r_] := 3 r Sqrt[x/(1 - x)] + 1/2 r^3 (x/(1 - x))^(3/2) - (3 r x Csch[r Sqrt[x/(1 - x)]])/(1 - x)
plotOptions = Sequence[AspectRatio -> Automatic, FrameLabel -> {"x", "r"}, PlotTheme -> {"Scientific", "LargeLabels"}];
ContourPlot[f[x, r] == 0, {x, 0.5, .999}, {r, 0, 1}, PlotPoints -> 100, Evaluate[plotOptions]]
Well, one also can solve it, numerically
rRoot[x_] := NSolve[f[x, r] == 0, r, Reals][[1, 1]]
data = rRoot~ParallelMap~Subdivide[.5, .999, 400] // Values;
ListLinePlot[data, DataRange -> {0.5, .999}, PlotRange -> {0, .9}, plotOptions]
Try to solve them numerically using FindRoot. You may do it as follows.Here is your equation:
eq = 3 r Sqrt[x/(1 - x)] +
1/2 r^3 (x/(1 - x))^(3/2) - (3 r x Csch[r Sqrt[x/(1 - x)]])/(1 -
x) == 0
This is the numerical solution returning the nested list with the element {x,r} , where r is the solution corresponding to this x vaue:
lst = Table[{x,
FindRoot[
3 r Sqrt[x/(1 - x)] +
1/2 r^3 (x/(1 - x))^(3/2) - (3 r x Csch[
r Sqrt[x/(1 - x)]])/(1 - x) == 0, {r, 1}][[1, 2]]}, {x,
0.5, 0.9, 0.01}];
Now, plotting it yields
ListPlot[lst,
AxesLabel -> {Style["x", 16, Italic], Style["r", 16, Italic]}]
That's it. I did not check, if the solution is single, ot there are several. It is up to you. If this is the case, play with the initial guess for the FindRoot to reveal other solutions.
Have fun!
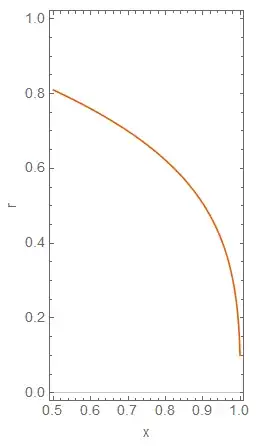
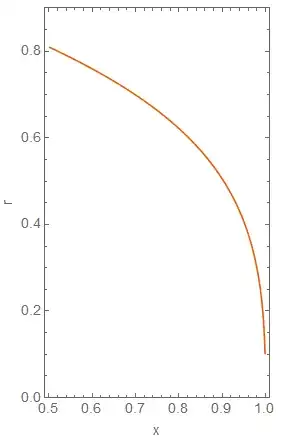
ContourPlot[ 3 r Sqrt[x/(1 - x)] + 1/2 r^3 (x/(1 - x))^(3/2) - ( 3 r x Csch[r Sqrt[x/(1 - x)]])/(1 - x) == 0, {x, 0.5, 1}, {r, 0, 1}]. – Αλέξανδρος Ζεγγ Dec 05 '18 at 12:01