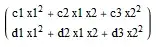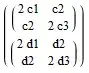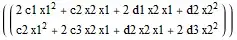Hessian matrix product in Taylor expansion of vector function

Question

I am trying to get the 2nd order coefficient of the Taylor expansion at $\pmb{x}=\pmb{0}$ of

f[{x1_, x2_}] = {{c1 x1^2 + c2 x1 x2 + c3 x2^2}, {d1 x1^2 + d2 x1 x2 + d3 x2^2}}

so, taking these notes into account, I calculated the Hessian matrix,

x1 /: Dt[x1, x2] = 0;
x2 /: Dt[x2, x1] = 0;

H = Dt[f[{x1, x2}], {{x1, x2}, 2},Constants -> {c1, c2, c3, d1, d2, d3}]
(* {{{{2*c1, c2}, {c2, 2*c3}}}, {{{2*d1, d2}, {d2, 2*d3}}}} *)

and, as described in the notes, multiplied it by $\pmb{x^T}$ on the left and $\pmb{x}$ on the right

X = {{x1}, {x2}}

Expand[X\[Transpose].H.X]
(* {{{{2*c1*x1^2 + c2*x2*x1 + 2*d1*x2*x1 + d2*x2^2}, {c2*x1^2 + 2*c3*x2*x1 + d2*x2*x1 + 2*d3*x2^2}}}} *)

but the result is not as expected, as it should be equal to $\pmb{f}$ (ignoring the 1/2 factor).

I think I followed Mathematica's matrix/vector product rules, so what am I missing?

Note: I am aware there are other simpler solutions such as

Normal[Series[f[{(x1 - 0) t, (x2 - 0) t}], {t, 0, 2}]] /. t -> 1
(* {c1 x1^2+c2 x1 x2+c3 x2^2,d1 x1^2+d2 x1 x2+d3 x2^2} *)

but I still want to know what I might have done wrong.

Answer 1

Since f is vector-values, you should better multiply from the right:

f[{x1_, x2_}] = {{c1 x1^2 + c2 x1 x2 + c3 x2^2}, {d1 x1^2 + d2 x1 x2 + d3 x2^2}};
H = D[f[{x1, x2}], {{x1, x2}, 2}];
X = {x1, x2};
f[X] == 1/2 (H.X).X // Expand

True

Answer 2

One problem (or difference from the notes) is that your function f[] is matrix-valued instead of scalar-valued. Your H turns out to be a matrix of Hessian matrices. Your method of computing the Hessian turns out to replace each scalar component of f[{x1, x2}] by its Hessian matrix. To recover f[], you need to apply Dot[] at the appropriate level.

Another difference is that X is a matrix (depth-2 array) instead of a vector (depth-1 array). While there is a natural isomorphism from $(2\times1)$-matrices to $2$-vectors, programmatically it makes a difference, since X\[Transpose].mat.X results in a $1\times1$ matrix {{q}} instead of a scalar q.

So H turns out to be a $2 \times 1$ matrix whose entries are $2 \times 2$ matrices.

Dimensions[H]
(*  {2, 1, 2, 2}  *)

The entries are the Hessian matrices h of the corresponding scalar entry of f[].

Addressing the first point, we can apply X\[Transpose].h.X/2 to each Hessian component matrix h by using Map. The entries h of the matrix H are at level 2. The following then gets the Dot[] product right:

Map[Expand[X\[Transpose].#.X/2] &, H, {2}]
(*  {{{{c1 x1^2 + c2 x1 x2 + c3 x2^2}}}, {{{d1 x1^2 + d2 x1 x2 + d3 x2^2}}}}  *)

The following breaks down the computation and illustrates the parts, which can get lost in the braces; pr[] prints each Dot[] result and highlights them in red:

pr[result_] := (Print["res -> ", result, ", dim -> ", 
    Dimensions[result]]; Style[result, Red]);
Map[pr@Expand[X\[Transpose].#.X/2] &, H, {2}] // MatrixForm

The above shows that output as a $2 \times 1$ matrix with $1 \times 1$ matrix entries.

That's why the OP's code wasn't working. The principal problem is making X a matrix instead of a vector. One might wonder whether the function f[] should be matrix- or vector-valued, since most vectors in the question appear as column matrices; but both types of functions are valid. If we use a vector, Dot[] contracts the last level of the tensor H:

X2 = {x1, x2};
H.X2 // Dimensions
H.X2.X2 // Dimensions
(*
  {2, 1, 2}
  {2, 1}
*)

The product H.X2.X2/2 is practically equivalent to use of Map at level {2}, but has the desired dimensions and is equal to f[X2]. This is the solution that @Henrik shows in his answer.