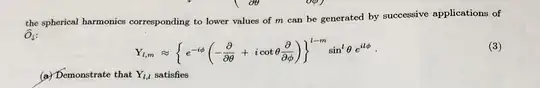Lowering operator for spherical harmonics

Question

I need to be able to generate all of the $ l=2 $ spherical harmonics using the lowering operator. The specific question is listed below. Any assistance would be much appreciated!

Thanksenter image description here

And how is this to the Wolfram Mathematica, the software to which this Q&A site is dedicated? — Henrik Schumacher, Dec 12 '18 at 23:18
You might have better luck on math.stackexchange or maybe physics.stackexchange. Unless you specifically want to do this using Mathematica. — b3m2a1, Dec 12 '18 at 23:36

Bob Hanlon · Answer 1 · 2018-12-13T18:42:37.337

3

Y[l_, m_] := 
 Y[l, m] = Nest[Simplify[Exp[-I*ϕ] (-D[#, θ] + 
        I*Cot[θ]*D[#, ϕ])] &, Sin[θ]^l*Exp[I*l*ϕ], l - m]

(table1 = Table[Y[l, m], {l, 0, 2}, {m, 0, l}]) // Grid[#, Frame -> All] &

Or

(table2 = table1 // TrigReduce) // Grid[#, Frame -> All] &

EDIT: As suggested by Alex Trounev, compare with the built-in SphericalHarmonicY

Table[SphericalHarmonicY[l, m, θ, ϕ], {l, 0, 2}, {m, 0, l}] // 
  Grid[#, Frame -> All] &

EDIT 2: For clarity, look at the ratio of the two functions

Table[SphericalHarmonicY[l, m, θ, ϕ]/Y[l, m], {l, 0, 5}, {m, 0, l}] // 
  Simplify // Grid[#, Frame -> All] &

edited Dec 13 '18 at 18:42

answered Dec 13 '18 at 03:44

Bob Hanlon

157,611
7
77
198

Bob can you add for comparison Table[SphericalHarmonicY[l, m, \[Theta], \[Phi]], {l, 0, 2}, {m, 0, l}] // Grid[#, Frame -> All] & – Alex Trounev Dec 13 '18 at 11:55

Lowering operator for spherical harmonics

1 Answers1