Problem with FindShortestTour function

Question

I'm new to Mathematica but I've read some documentation and guides and, unfortunately, haven't found a solution.

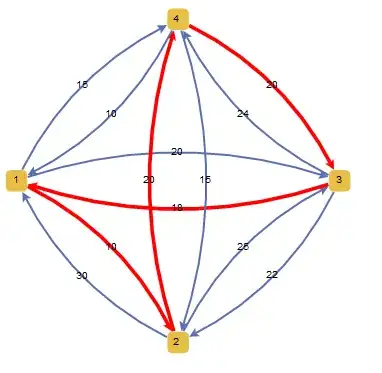
There's the following matrix in the task:

And I have to solve this TSP problem specifically with the help of FindShortestTour function. Not FindShortestPath or sth else.

I have tried several variants, but if I do something like this:FindShortestTour[{{\[Infinity], 10, 20, 15}, {30, \[Infinity], 25, 20}, {18, 22, \[Infinity], 24}, {10, 15, 20, \[Infinity]}}] I get a mistake: The distance function EuclideanDistance does not give a numerical result when applied to two points. I guess that's because of Infinity symbols inside a matrix.

It is said, that "Infinity means no edge between vertices." TSP - travelling salesman problem. — Drew.V, Dec 17 '18 at 12:03
Possible duplicate of this. See if one of those answers helps you out. — bobthechemist, Dec 17 '18 at 12:05
I tried to solve it like in th link you provided, but the solution wasn't right. — Drew.V, Dec 17 '18 at 12:15

score 2 · Answer 1 · answered Dec 17 '18 at 11:59

2

Just replace ∞ by 0:

A = {{∞, 10, 20, 15}, {30, ∞, 25, 20}, {18, 22, ∞, 24}, {10, 15, 20, ∞}} ;
FindShortestTour[A/. ∞ -> 0]

Actually, a distance matrix in which a vertex has infinite distance does not make sense.

{5 Sqrt[14] + 5 Sqrt[42] + 3 Sqrt[141] + Sqrt[949], {1, 4, 2, 3, 1}}

answered Dec 17 '18 at 11:59

Henrik Schumacher

106,770
7
179
309

It is asid, that "Infinity means no edge between vertices". And yeah, I tried to replace it with 0, but the result is still wrong :( – Drew.V Dec 17 '18 at 12:01

bobthechemist · Answer 2 · 2018-12-17T12:25:22.293

0

Too long for a comment. I've cut and pasted the code from this answer so go upvote that instead.

d = SparseArray[{{1, 2} -> 10, {1, 3} -> 20, {1, 4} -> 15, {2, 1} -> 
     30, {2, 3} -> 25, {2, 4} -> 20, {3, 1} -> 18, {3, 2} -> 
     22, {3, 4} -> 24, {4, 1} -> 10, {4, 2} -> 15, {4, 3} -> 20}, {4, 
    4}, Infinity];
{len, tour} = 
 FindShortestTour[{1, 2, 3, 4}, DistanceFunction -> (d[[#1, #2]] &)]
HighlightGraph[
 WeightedAdjacencyGraph[d, GraphStyle -> "SmallNetwork", 
  EdgeLabels -> "EdgeWeight"], 
 Style[DirectedEdge[#1, #2], Thickness[.01], Red] & @@@ 
  Partition[tour, 2, 1, 1]]

edited Dec 17 '18 at 12:25

answered Dec 17 '18 at 12:14

bobthechemist

19,693
4
52
138

THAT'S IT! Thank you so much! – Drew.V Dec 17 '18 at 12:16
Do note that the C&P solution complains because your matrix is not symmetric. Also, I don't get the fancy highlighted path. I don't know enough about the graph functions to know why this is the case. Caveat Emptor. – bobthechemist Dec 17 '18 at 12:20
Shamelessly seeking a hat, can you accept this answer without voting it up? – bobthechemist Dec 17 '18 at 12:58

Problem with FindShortestTour function

2 Answers2