Defining a function with a point of finite discontinuity

Question

I wrote the code for the function $T$ defined on $[0,1]$ by $T(x)=\frac{x+2}{3}$ if $x\neq\frac{1}{2}$ and $T(\frac{1}{2})=1$ as follows.

T[x_] := If[x != 1/2, (2*x + 1)/3, 1];

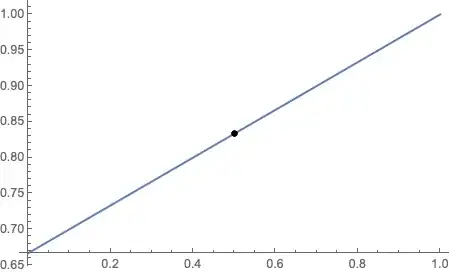
I am not sure if the code I wrote defines the function $T$ correctly as the command `Plot' fails to highlight the discontinuity at $\frac{1}{2}$.

A clarification to my doubt will be highly appreciated. Thanks!

You can format inline code and code blocks by selecting the code and clicking the {} button above the edit window. The edit window help button ? is useful for learning how to format your questions and answers. You may also find this meta Q&A helpful — Michael E2, Dec 17 '18 at 14:47
Possible duplicate of Plot a piecewise function with black and white disks marking discontinuities — march, Dec 19 '18 at 17:25

score 2 · Answer 1 · edited Dec 17 '18 at 16:56

2

f[x_] := Piecewise[{{(x + 2)/3, x != 1/2}, {1, x == 1/2}}]
Plot[f[x], {x, 0, 1}, 
 ExclusionsStyle -> {Dotted, Directive[Black, AbsolutePointSize[5]]}]

edited Dec 17 '18 at 16:56

Bob Hanlon

157,611
7
77
198

answered Dec 17 '18 at 15:19

Rohit Namjoshi

10,212
6
16
67

@Bob Hanlon. Thanks for fixing my typo. – Rohit Namjoshi Dec 17 '18 at 17:01
1

To show the actual value at the discontinuity: Plot[f[x], {x, 0, 1}, ExclusionsStyle -> {Dotted, Directive[White, AbsolutePointSize[3]]}, Epilog -> {Red, AbsolutePointSize[5], Point[{1/2, f[1/2]}]}] – Bob Hanlon Dec 17 '18 at 17:05

Defining a function with a point of finite discontinuity

1 Answers1