How can I make a convex catenoid (minimum surface of revolution that closes on -1 and 1?

Question

In Wolfram MathWorld I see the catenoid (minimum surface of revolution which is concave and open ended, but I want the one where the sides are convex and close on the long axis (say z) at -1 and 1.

I want to start with the "rope-hanging" catenary of the hyperbolic cosine and also show the exp functions for e that average on the cosh x, as if the catenoid function is defined in a 3d exp field forming a space around the axis.

Then I think there is an interesting relation between the surface area and volume, because of the interesting derivative properties on the cosh x function.

I'm hope this is simple modification of the concave equations. This figure shows my general idea. Here I moved the exp function to the endpoints because it is less confusing.

What exactly is the question? The minimum surface of revolution that is closed will be a straight line, which is not very interesting, so please clarify what precisely you're after. — Lukas Lang, Jan 02 '19 at 16:31
No, the minimum surface of resolution will not be a line because it has curvature a, as in this graph. So it should be shaped like a "cigar" and the exp functions come form the middle of the fusiform volumetric which is a circle in the x-y plane. The idea is this models the first mode of a vibrating string. I could use the second mode, too, which has a nodal point in the middle, but that needs a different catenary I don't have. — Terence B Allen, Jan 02 '19 at 23:00
@TerenceBAllen please see https://mathematica.stackexchange.com/help/merging-accounts — Kuba, Jan 03 '19 at 08:01
Are you wanting to get a minimal surface for constant volume (and to plot geometric properties such as volume, curvature, area) or are you just wanting to visualise surfaces of revolution from your equations? — Dunlop, Jan 04 '19 at 06:30

score 2 · Answer 1 · answered Jan 06 '19 at 03:56

I am writing this answer to address a misconception you seem to have.

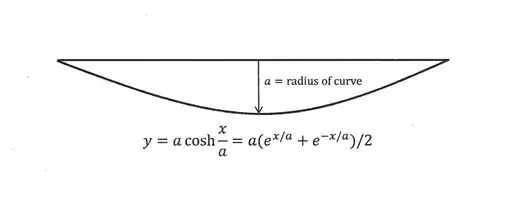
First, let us generate a general formula for your surface of revolution. The idea is to rotate the shifted catenary $y=k+\cosh x$ over the $x$-axis, with the shift $k$ determining the appearance of the surface of revolution:

catrev[k_, {x_, θ_}] := {x, (k + Cosh[x]) Cos[θ], (k + Cosh[x]) Sin[θ]}

In particular, the cigar-shaped surface you imply in the OP corresponds to the value k = -Cosh[1]:

ParametricPlot3D[catrev[-Cosh[1], {x, θ}], {x, -1, 1}, {θ, 0, 2 π}]

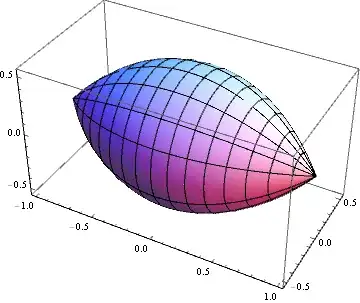
surface

Let us determine the surface area and volume of a generalization of these "cigars", by first letting $k=-\cosh h$.

(* surface area *)
Assuming[h > 0, 
         RegionMeasure[{x, (Cosh[x] - Cosh[h]) Cos[θ], (Cosh[x] - Cosh[h]) Sin[θ]},
                       {{x, -h, h}, {θ, 0, 2 π}}]]
   π (-2 h + Sinh[2 h])

(* volume *)
Assuming[h > 0, 
         Volume[{x, c (Cosh[x] - Cosh[h]) Cos[θ], c (Cosh[x] - Cosh[h]) Sin[θ]},
                {c, 0, 1}, {x, -h, h}, {θ, 0, 2 π}]]
   π (2 h + h Cosh[2 h] - 3 Cosh[h] Sinh[h])

I think there is an interesting relation between the surface area and volume...

I'm not seeing a particularly simple one, myself.

Now, for your misconception. A minimal surface is a very specific concept in differential geometry; it refers to a surface with zero mean curvature. Qualitatively speaking, minimal surfaces will be either flat like the plane, or concave almost everywhere. Your proposed cigars fit neither of these appearances.

More concretely, let's determine the mean curvature of the surface of revolution constructed above:

MeanCurvature[f_?VectorQ, {u_, v_}] := 
  Simplify[(Det[{D[f, {u, 2}], D[f, u], D[f, v]}] D[f, v].D[f, v] - 
            2 Det[{D[f, u, v], D[f, u], D[f, v]}] D[f, u].D[f, v] + 
            Det[{D[f, {v, 2}], D[f, u], D[f, v]}] D[f, u].D[f, u])/
           (2 PowerExpand[Simplify[(D[f, u].D[f, u] D[f, v].D[f, v] -
                                    (D[f, u].D[f, v])^2)]^(3/2)])]

(definition taken from here)

With that,

MeanCurvature[catrev[k, {x, θ}], {x, θ}]
   -((k Sech[x]^2)/(2 (k + Cosh[x])))

and it is clear that this can only be zero if k == 0, which is exactly the catenoid case.

How can I make a convex catenoid (minimum surface of revolution that closes on -1 and 1?

1 Answers1