I am looking for some tips or guidance as to what machinery in mathematica can help me get at this problem numerically. I am looking for fixed points of a mapping, but the objects in question are themselves functions. Hence I am looking for a fixed point function.
The setup (simplified version): suppose we restrict our search to continuous functions $f: [0,1]\rightarrow [0,1]$. $p$ is a known parameter. I am looking for a fixed point (function) such that, for all $x\in [0,1]$, $f(x)$ solves
$$f(x) = \frac{x^p}{x^p + \int_0^1 f(x) x^p \, dx }.$$
It's not as simple as finding lots of fixed points for each $x$ in isolation, as the value of the expression at a single $x$ depends on the entire function $f$. Any help to try and solve this type of thing numerically would be much appreciated.

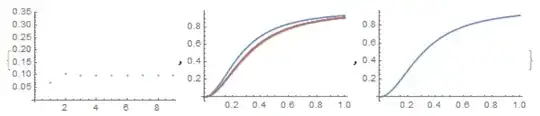
Eigenvalueproblem which can be solved withEigensystemorNDEigensystem. -useInterpolationas function representation and sample and reinterpolate after each iteration. - use a variational approach to find the fixed point, perhaps theVariationalMethodspackage can help with that. – Thies Heidecke Jan 03 '19 at 13:47DSolve, numerically byNDSolveor iteratively by a Picard iteration. I'm not sure if all of those methods can successfully tackle your problem, but all those alleys could be explored in Mathematica. Hope this gives you some ideas! When you try something and need further help, update your question with Mathematica code and specific questions, so that people can help you with the details.I have tried the ODE approach. I don't think that it can be transformed into an ODE as I don't see a way to remove the integral. The ratio means it can't be transformed into a Fredholm equation, for which code already exists to numerically solve.
I will try discretizing in line with the great answer below. And I am a little lost by your suggestion, Lukas, although I will try work through it as well.
– user434180 Jan 03 '19 at 14:38