Picking mesh elements that are not on the border of the mesh

Question

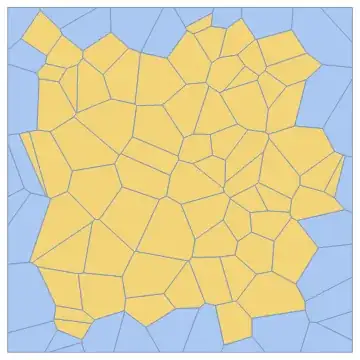
As an example, let's say I use a set of random points to create a Voronoi mesh

pts = RandomReal[{-1, 1}, {100, 2}];
VoronoiMesh[pts, {-1, 1}]

and get something that looks like this:

My question is: Is there an efficient way to determine which of the regions (mesh elements, whatever you call them) are not touching the edge of the mesh? I know that there are a lot of built in functions that give properties of elements in a mesh, but I am unfamiliar with them, and I can't seem to find an efficient way to do this beyond "looping" through all elements and just picking which elements do not have points that touch the edge.

RegionBoundary? To get coordinates you can do RegionBoundary@mesh // MeshCoordinates — b3m2a1, Jan 07 '19 at 22:45
@b3m2a1 I mean to find the "shapes" that are not touching the outside. I don't need the coordinates of the outer edge. — BioPhysicist, Jan 07 '19 at 22:52
Ah I did a lazy read through and figured you wanted the boundary. Always possible to take a complement with the boundary cells, though, to get the interior. — b3m2a1, Jan 07 '19 at 22:53

kglr · Accepted Answer · 2019-01-07T22:56:37.070

10

vm = VoronoiMesh[pts, {-1, 1}]
HighlightMesh[vm, MeshCellIndex[vm, {2, "Interior"}]]

Related: Boundary cells of a mesh?

Show[vm, Epilog -> {Opacity[.7, Orange], MeshPrimitives[vm, {2, "Interior"}]}]

edited Jan 07 '19 at 22:56

answered Jan 07 '19 at 22:52

kglr

394,356
18
477
896

Yep that was the simple answer I was expecting haha. Thanks! – BioPhysicist Jan 07 '19 at 22:55
2

@kglr Wow, I'm impressed. Where did you find this syntax? The doc page of MeshCellIndex does not show it as example... – Henrik Schumacher Jan 07 '19 at 23:29
1

@HenrikSchumacher, blind search trying some objects returned by vm["Properties"]:) – kglr Jan 08 '19 at 00:00
@HenrikSchumacher Exactly what I was thinking! I'll definitely look at those properties though and see if there are other useful things. – BioPhysicist Jan 08 '19 at 12:45

score 8 · Answer 2 · answered Jan 07 '19 at 22:46

For planar MeshRegion that arise from DelaunayMesh or VoronoiMesh, usually

R["InteriorFaces"]

should work.

A more general and more transparent ways is to use the package "IGraphM`" by Szabolcs as follows:

Needs["IGraphM`"]

A = IGMeshCellAdjacencyMatrix[R, 1, 2];
bndedges = Random`Private`PositionsOf[Total[A, {2}], 1];
interiorfaces = Random`Private`PositionsOf[Total[A[[bndedges]]], 0];

HighlightMesh[R, Thread[{2, interiorfaces}]]

Picking mesh elements that are not on the border of the mesh

2 Answers2

Linked