I am trying to plot a set of layers with different values of densities (density profile). Geometry ({x,z} values) of 15 interfaces of layers look like this:

while the first interface is a planar surface. {x, z} values and densities of individual interfaces can be found here.
I tried to use ArrayPlot. Here is my attempt:
(*read data*)
ninterf = 15;
interfaces =
Table[Import["interface_" <> ToString[i] <> ".dat", "Table"], {i, 1,
ninterf}];
densities = Flatten[Import["den.dat", "Table"]];
rangex = MinMax[#[[1]] & /@ interfaces[[1]]]
rangez = {Min[#[[2]] & /@ interfaces[[-1]]],
Max[#[[2]] & /@ interfaces[[1]]]}
(*interpolate data*)
f = Table[Unique[f$], {i, 1, ninterf}];
Table[f[[i]] = Interpolation[interfaces[[i]], InterpolationOrder -> 1], {i,
1, ninterf}];
F = Through@*f;
(*create a grid of {x,z} values for ArrayPlot*)
step = 1.;
xzvalues =
Table[{N[i], N[j]}, {i, rangex[[1]], rangex[[2]], step}, {j,
rangez[[2]], rangez[[1]], -step}];
(*determine density for every point of the grid*)
densityfunc[xval_, zval_] :=
Module[{numb =
Last[Flatten[Position[F[N[xval]], _?(# >= N[zval] &)]]]},
densities[[numb]]];
values = Apply[densityfunc, #, {1}] & /@ xzvalues;
(*Show result-ArrayPlot*)
ArrayPlot[Transpose[values], ColorFunction -> "Rainbow"]
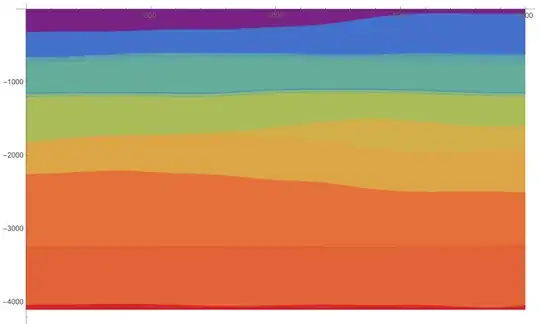
Here is the final picture-density profile
The time needed for calculation of values on my computer is 689.04 seconds (for bigger models, e.g. 5 times bigger, this might take a lot of time). In this case, I set the grid spacing step=1. since interfaces should look smooth. With bigger step the calculation time would be shorter but interfaces would not be smooth enough.
I would like to speed up the evaluation of values(if it is possible; parallelization of code would be also welcomed) or maybe someone knows faster way how to get similiar picture of density profile. I will be grateful for any suggestions.
UPDATE: Carl Lange and kglr proposed using Filling which works great for this simple model of 15 interfaces. Could be Filling used also for this complex model of layers?

The data for this complex model can be found here.

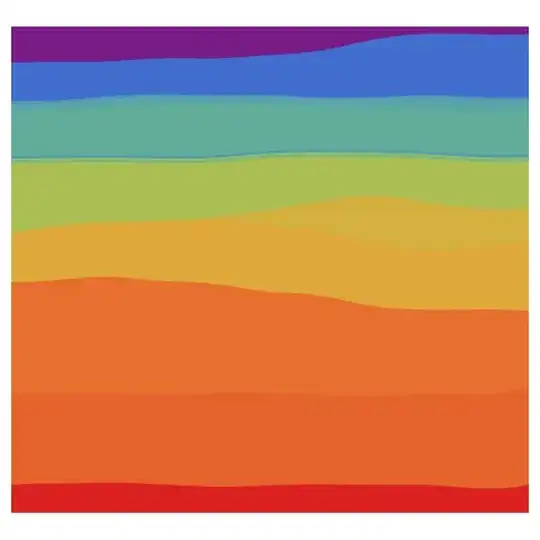




Filling, but I think I'm just misunderstanding your exact problem and intention. – Carl Lange Jan 17 '19 at 14:17Filling.Thank you. Yes, in this case it solves my problem. I just need to think about it little more. Maybe is not applicable for all configurations (more complex density profiles). – Moonwalk Jan 17 '19 at 14:36