Update:
Counts[data] seems to be equivalent to AssociationThread @@ Transpose@Tally[data]. The OP's problem arises because in constructing an Association, keys are checked for uniqueness and later entries with a duplicate key replace earlier entries. (Simple example: Association[{1. -> 1, 1. -> 2}].) Uniqueness is determined by MatchQ, I believe, which has problems discussed below in the original answer. The problem with SameQ not strictly being an equivalence relation due nontransitivity is still an issue. This update principally clarifies the role of forming an association: It discards entries of the Tally with duplicate keys, which results in an undercount.
Original answer:
Working with floating-point numbers is tricky. I'd say the most important, common issue is that rounding errors lead to different but close numbers that users wish would be treated the same. Introductory programming courses teach that comparing floats should be done with something like Abs[x - y] < $MyTolerance. In Mathematica similar (but relative) tolerances are built into SameQ and Equal, which are controlled by the the internal system parameters Internal`$SameQTolerance and Internal`$EqualTolerance respectively (see also this; this question has similar issues as the OP). Perhaps less well known is that MatchQ has a small tolerance like SameQ but is slightly more restrictive. The most important difference is that MatchQ is transitive but SameQ is not.
These functions play various roles in pattern-matching and comparing numbers, and their issues affect functions like Counts[] when applied to floating-point data. When constructing classes from data, as in Counts[], some reflection should lead one to think that using a comparison that is an equivalence relation, and therefore transitive, would be desirable. And if not transitive, it should be at least "locally transitive" on the actual data being used. By "locally transitive," I mean that the relation is transitive when restricted to the data set, even if it is not transitive on all floating-point numbers.
This seems to be the problem with the OP's example: SameQ is not transitive on xs. I say "seems" because I cannot check the internal workings of Counts[]. It's possible that SameQ is used to construct the keys and MatchQ to tally the counts. It seems to me that Counts[] uses SameQ and CountsBy[] uses MatchQ to construct the keys, however the counting is done. Since SameQ is not transitive, the order that the data is processed can make a difference. Nevertheless, the problem can be fixed by making SameQ locally transitive on xs.
The reason this comes up in this example is that in constructing the data xs, the rounding drift amounts to 2 bits (2 ulp), which is one too many for SameQ to be locally transitive.
Here is the best fix (that fixes SameQ -- Chip Hurst points out that the tolerance can be as small as 0.55, which is close to the value of Log10[4.] = 0.60.. that would be predicted by the observed rounding error):
Block[{Internal`$SameQTolerance = Internal`$EqualTolerance},
Total@Counts[xs]]
(* 100 *)
Another fix is to use MatchQ via CountsBy[]:
Total@CountsBy[xs, # &]
(* 100 *)
The CountsBy[] association has several keys for equal numbers, but it does have the correct total. The first solution seems better because it has one key for each cluster of equal numbers. (It likely that in some applications one would like distinct floating-point numbers to have distinct entries; then something like CountsBy[xs, ToString@*FullForm] would do the trick.)
Appendix
Some pictures showing the properties of SameQ and MatchQ on consecutive machine-precision floats:
Block[{x1},
x1 = Table[1 + n*$MachineEpsilon, {n, 0, 5}];
{Outer[Boole@*SameQ, x1, x1] // MatrixPlot[#, PlotLabel -> SameQ] &,
Outer[Boole@*MatchQ, x1, x1] // MatrixPlot[#, PlotLabel -> MatchQ] &} //
GraphicsRow
]


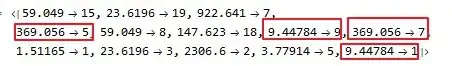

Tallydoes not have the same problem.) – Alan Jan 20 '19 at 16:45assoc = AssociationThread[xs -> Range[Length[xs]]]. – kglr Jan 20 '19 at 16:55CountsandTotal[AssociationThread @@ Transpose[Tally[xs]]]is9.44784`. The fact that it's present inTally[xs], but not the association form led me to believe it's impossible to have both9.44784`and9.447839999999998`as keys in the same association... but that's not the case as they're both present withMerge[Association[{# -> 1}] & /@ xs, Total]. – Greg Hurst Jan 20 '19 at 17:00Block[{$Internal`SameQTolerance = 0.55}, Total[Counts[xs]]]fixes this particular example. – Greg Hurst Jan 20 '19 at 17:11Countsshd be expected to be as intelligent asTally.) – Alan Jan 20 '19 at 17:279.44784`and9.447839999999998`are not both present inMerge[Association[{# -> 1}] & /@ xs, Total], which seems to be different than what you are saying. – Michael E2 Jan 21 '19 at 18:336instead of8now... `In[18]:= $OperatingSystemOut[18]= "MacOSX"
In[19]:= Merge[Association[{# -> 1}] & /@ xs, Total] // Keys
Out[19]= {59.048999999999985, 23.6196, 922.640625, 369.05625000000003, 59.049, 147.6225, 9.44784, 369.05625, 1.5116543999999998, 23.61959999999999, 2306.6015625, 3.7791359999999994, 9.447839999999996}`
– Greg Hurst Jan 21 '19 at 20:03"11.3.0 for Mac OS X x86 (64-bit) (January 22, 2018)"-- I got what you're now showing. My theory is that becauseMatchQ[9.44784`, 9.447839999999998`]returnsTrue, they're treated as the same key. – Michael E2 Jan 21 '19 at 20:169.447839999999998came from. – Greg Hurst Jan 21 '19 at 20:17