1

I solved the following heat equation PDE analytically by hand and also Maple the solutions were the same.

Also, I solved the PDE numerically using Maple. But the analytic solution and numerical solution plots are different with each other! Why?! And which one is correct?

For validating Maple's numerical solution, I solved the PDE using Mathematica (NDSolve) ,too and it gave me the same plot as Maple's numerical plot. \begin{equation}u_{t}-u_{xx}=0\end{equation}

\begin{equation}0<x<\pi\end{equation}

\begin{equation}t>0\end{equation}

Boundary Conditions:

\begin{cases}u(0,t)+u_{x}(0,t)=1\\u(\pi,t)+u_{x}(\pi,t)=-1\end{cases}

Initial Condition:

\begin{equation}u(x,0)=sin(x)\end{equation}

Maple analytic solution and code:

PDE3 := {u(0, t)+(D[1](u))(0, t) = 1, u(Pi, t)+(D[1](u))(Pi, t) = -1, diff(u(x, t), x$2) = diff(u(x, t), t), u(x, 0) = sin(x)};
sol3 := `assuming`([pdsolve(PDE3)], [0 < x and x < Pi, t > 0]);
plot3d(subs(infinity = 1000, rhs(sol3)), x = 0 .. Pi, t = 0 .. 0.5e-1);

enter image description here

Maple numerical code:

PDE4 := {diff(u(x, t), x$2) = diff(u(x, t), t)}
IBC := {u(0, t)+(D[1](u))(0, t) = 1, u(Pi, t)+(D[1](u))(Pi, t) = -1, u(x, 0) = sin(x)}
sol4 := pdsolve(PDE4, IBC, numeric)
plot3d(subs(infinity = 1000, rhs(sol3)), x = 0 .. Pi, t = 0 .. 0.5e-1)

Maple Analytic Solution Plot:

enter image description here

Maple Numerical Solution Plot:

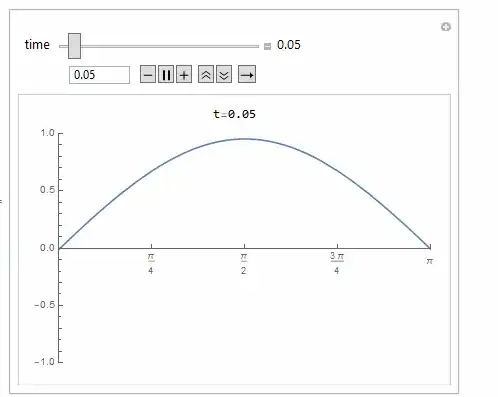
enter image description here

Mathematica Numerical Solution Plot:

enter image description here

Moreza7
  • 83
  • 5
  • Add Wolfram code for your Mathematica plot. At first glance it seems you just need to add the BoxRatios -> 1 option to your Mathematica plot. – Edmund Jan 24 '19 at 01:00
  • @Edmund There is no problem with Mathematica's plot that's just for validating the Maple's numerical solution. The Mathematica's plot validates the numerical solution plot of Maple. The problem is: Why numerical and analytical plots are different? – Moreza7 Jan 24 '19 at 01:13
  • Since 2 out of 3 approaches agree, I'd guess the Maple analytical solution is wrong :) Actual evidence: it doesn't look like the Maple analytical solution matches the initial conditions. – Chris K Jan 24 '19 at 02:01
  • 5
    I'm voting to close this question as off-topic because it's more of a Maple question than a Mathematica question. – Chris K Jan 24 '19 at 03:35
  • 1
    Side note: With the help of LaplaceTransform and easyFourierTrigSeries, it's possible to show a correct series solution is $$e^{-t} \sin (x)-\frac{e^{-t}}{\pi }-\frac{e^t}{\pi }+\frac{4}{\pi } \left(\frac{\pi }{4}-\frac{x}{2}\right)+\frac{2}{\pi }-\frac{4}{\pi } \sum _{k}^{\infty } \left(\frac{e^{-4 k^2 t} (2 k \cos (2 k x)-\sin (2 k x))}{2 k \left(-1+4 k^2\right) \left(1+4 k^2\right)}+\frac{e^{-t} (-\cos (2 k x)+2 k \sin (2 k x))}{2 \left(-1+4 k^2\right)}+\frac{e^t (\cos (2 k x)+2 k \sin (2 k x))}{2 \left(1+4 k^2\right)}\right)$$ – xzczd Jan 24 '19 at 07:45
  • @xzczd Thank you! But it's not the right solution ,too. Because when I plot your solution with the following codes, the plot is not the same as numerical solution plot: maplesol = E^(-t)*Sin[x] - E^(-t)/Pi - E^(t)/Pi + (4/Pi) (Pi/4 - x/2) + (2/Pi) - 4/Pi + Inactivate[ Sum[((E^(-4 n^2 t) (2 n Cos[2 n x] - Sin[2 n x]))/(2 n (-1 + 4 n^2) (1 + 4 n^2))) + ((E^(-t) (- Cos[2 n x] + 2 n Sin[2 n x]))/(2 (-1 + 4 n^2))) + ((E^(t) (Cos[2 n x] + 2 n Sin[2 n x]))/(2 (1 + 4 n^2))), {n, 1, Infinity}]] – Moreza7 Jan 24 '19 at 10:57
  • You do not copy the fomula correctly. Notice it's $\frac{4}{\pi}×$ rather than $\frac{4}{\pi}+$. – xzczd Jan 24 '19 at 10:57
  • @xzczd Yes, you're right. Can you tell me how did you find this solution, please? – Moreza7 Jan 24 '19 at 11:04
  • The specific code is too long to show in the comment, but I've used essentially the same method in this, this and this answer, you may have a look. – xzczd Jan 24 '19 at 11:22
  • @xzczd Thank you. – Moreza7 Jan 24 '19 at 12:12
  • @xzczd I created a new topic that shows my own analytic solution which is not same as your solution. Would you please look at that? https://mathematica.stackexchange.com/questions/190169/why-my-solution-of-pde-is-not-compatible-with-mathematicas-numerical-solution – Moreza7 Jan 24 '19 at 12:33

1 Answers1

4

Maple analytical solution appears to be wrong. It does not even satisfy the initial conditions. Mathematica currently can not solve this PDE analytically (but this is better than solving it and giving wrong solution ;)

Here is side by side animation of Maple solution and Mathematica animated for one second.

Maple

restart;
PDE3 := diff(u(x, t), x$2) = diff(u(x, t), t):
ic:= u(x, 0) = sin(x):
bc:= u(0, t)+(D[1](u))(0, t) = 1, u(Pi, t)+(D[1](u))(Pi, t) = -1:
sol3 := pdsolve([PDE3,ic,bc],u(x,t)):
sol:=subs(infinity=20,rhs(sol3)):
plots:-animate(plot,[sol,x=0..Pi],t=0..1,frames=100)

Mathematica graphics

Mathematica

ClearAll[u,x,t];
pde=D[u[x,t],t]==D[u[x,t],{x,2}];
ic=u[x,0]==Sin[x];
bc={u[0,t]+Derivative[1,0][u][0,t]==1, u[Pi,t]+Derivative[1,0][u][Pi,t]==-1};
sol=NDSolve[{pde,ic,bc},u,{x,0,Pi},{t,0,1}]


Manipulate[
Grid[{{Row[{"t=",t}]},
{Plot[Evaluate[u[x,t]/.sol],{x,0,Pi},
 PlotRange->{{0,Pi},{-1,1}},ImageSize->300,
 Ticks->{{0,Pi/4,Pi/2,3/4 Pi,Pi},Automatic}]
}}],
{{t,0,"time"},0,1,.01,Appearance->"Labeled"}
]

Mathematica graphics

Animation

Maple

enter image description here

Mathematica

enter image description here

May be you can report this bug to Maplesoft.

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • Thank You! I posted a new question which shows my analytic solution of the problem which is not compatible with Mathematica's numerical solution again. Would you please look at that? https://mathematica.stackexchange.com/questions/190169/why-my-solution-of-pde-is-not-compatible-with-mathematicas-numerical-solution – Moreza7 Jan 24 '19 at 12:10