How do I plot x as a function of y?

Question

I am new to Mathematica, so this might be a silly question.

I'm in Calculus 2 and I'm doing this problem:

Use the cylindrical shells method to find the volume of the revolution of a region bounded by $x = 1+(y-2)^2$ , $x = 2$ about the $x$-axis

I know how to do this on paper but this course gives 75% credit, and 25% for a solution in Mathematica.

The problem I'm having is that when I try to plot $x = 1+(y-2)^2$ and $x = 2$ I'm really getting $y= 1+(x-2)^2$ and $y=2$ back

ex:

Plot[{1 + (y - 2)^2, 2}, {y, 1, 3}]

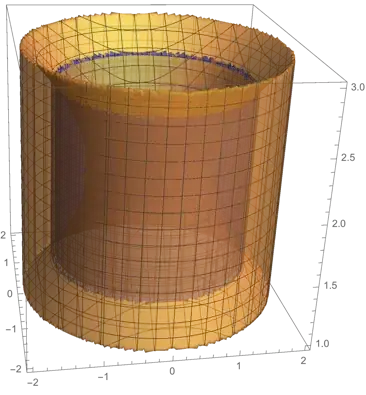
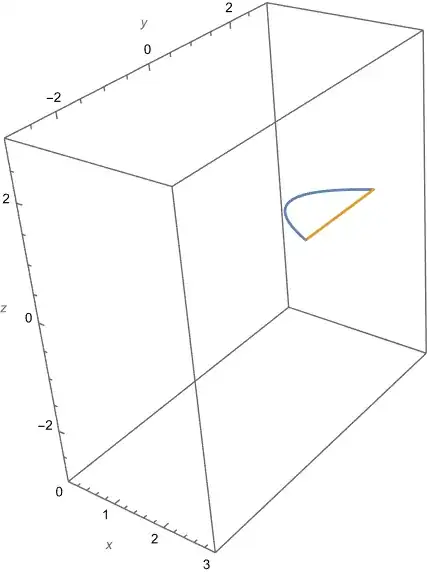
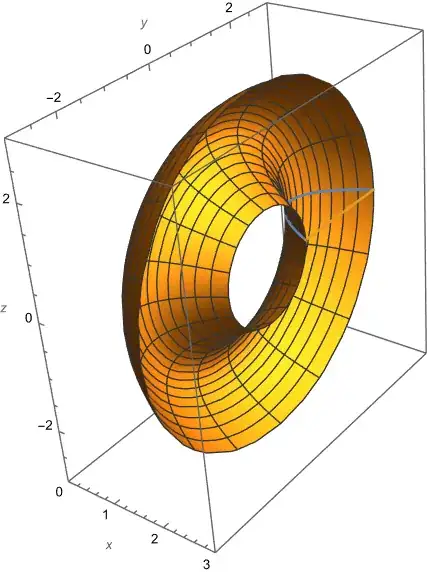
You have $x=2$ when $y\in[1,3]$. Therefore ParametricPlot[{1+(y-2)^2,y},{y,1,3}] will produce the most difficult part of the boundary. If you need to plot the surface of revolution also, use a polar coordinate in addition (and ParametricPlot3D). Anyway, using ParametricPlot(3D) gives you control of which coordinate is a function of the other(s). — Jyrki Lahtonen, Jan 24 '19 at 22:51
Possible duplicate: https://mathematica.stackexchange.com/questions/190196/how-do-i-plot-x-as-a-function-of-y-in-mathematica — Michael E2, Jan 25 '19 at 00:31
Possible duplicate: https://mathematica.stackexchange.com/questions/18655/how-can-i-transpose-x-and-y-axis-on-a-plot — Michael E2, Jan 25 '19 at 00:38
Duplicate of underlying volume problem: https://mathematica.stackexchange.com/questions/136610/volume-of-a-region-of-revolution — Michael E2, Jan 25 '19 at 00:46

score 2 · Answer 1 · answered Jan 24 '19 at 21:55

2

Not an answer, but figures to help you forward:

answered Jan 24 '19 at 21:55

David G. Stork

41,180
3
34
96

score 1 · Answer 2 · answered Feb 09 '24 at 13:35

ParametricPlot[{{1 + (y - 2)^2, y}, {2, y}}, {y, 1, 3}, 
 PlotRange -> {{0, 3}, {0, 3}}, AxesLabel -> {x, y}]

ParametricPlot3D[{{1 + (y - 2)^2, y, 0}, {2, y, 0}}, {y, 1, 3}, 
 PlotRange -> {{0, 3}, {-3, 3}, {-3, 3}}, AxesLabel -> {x, y, z}]

RevolutionPlot3D[{1 + (y - 2)^2, y, 0}, {y, 1, 3}, 
  RevolutionAxis -> {1, 0, 0}, 
  PlotRange -> {{0, 3}, {-3, 3}, {-3, 3}}, AxesLabel -> {x, y, z}];

Show[%%, %]

Region@ParametricRegion[{RotationMatrix[a, {1, 0, 0}] . {x, y, 
      0}, {x >= 1 + (y - 2)^2, x <= 2, 0 <= a < 2 π}}, {x, y, a}];

Show[%%, %]
Volume[%%]

16/3 π

How do I plot x as a function of y?

2 Answers2