I am trying to solve a second order equation of the form $u^{\prime \prime}(t)+\left(k^2-V(t)\right)u(t)=0$. However, since the $t$ we consider can be quite large ($10^{20}$ or higher) and the wavenumbers we are interested in lie in a very small region ($10^{-23}<k<10^{-16}$), we consider the variable $y=kt$ to get reasonable values.
This gives the equation $u^{\prime \prime}(y)+\left(1-V(y)\right)u(y)=0$, and I tried to solve it by breaking it into two first order equations $ x^{\prime}=p$ and $ p^{\prime}=V(y)-1$.
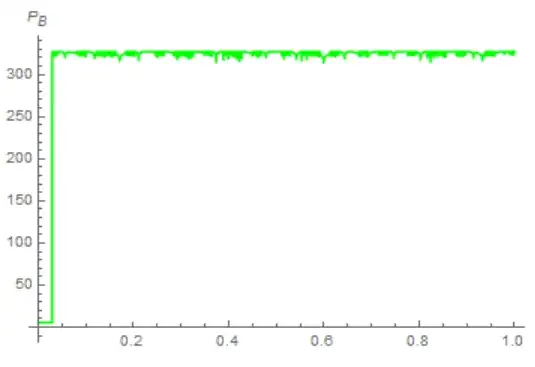
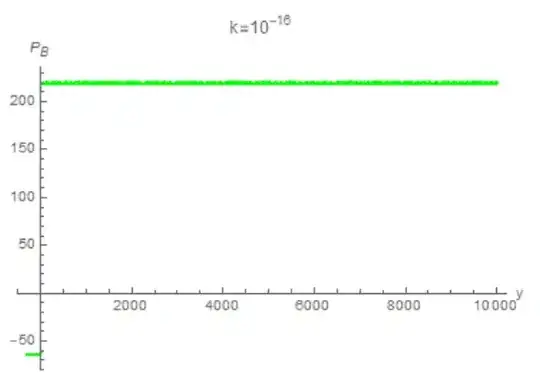
However, even after hours of running, the code does not produce an output for $k=10^{-16}$, and is very wrong for $k=10^{-23}$ (the power spectrum gives me just a lot of oscillations).
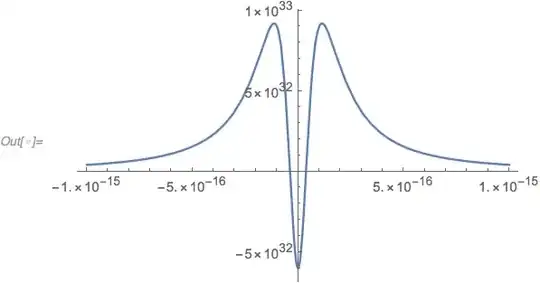
I suspect the problem comes from the rapidly varying potential near the origin. Plotting the potential for $k=10^{-2}$ as an example, it gives me the form I expect, but this breaks down for lower values (lower figure for $k=10^{20}$).
I have read from the NDSolve Stiffness tutorial that the stepsize will change automatically according to the problem, which may cause Mathematica to be very slow. Thus, I tried playing around with the different options but nothing came out. I know this has be done in Matlab, and the expected output should be something like this:
with the black curve the actual solution, while the other two represent power-law scalings.
Here is the code I use:
Clear["Global`*"];
$HistoryLength = 0;
ClearSystemCache;
(*Definition of the potential*)
χ = 10^(25);
ss[y_] := Sqrt[k^2 + y^2]
ss2[y_] := k^2 + y^2;
cst = 1370/χ;
a0[y_] := (cst*y/k)^2 + 2*cst*ss[y]/k;
a1[y_] := 2*cst*y (ss[y]*cst + k)/(ss[y]*k^2);
a2[y_] := 2 cst*(ss[y]*cst*ss2[y] + k^3)/(ss[y]*k^2*ss2[y]);
a3[y_] := -6*cst*k*y/(ss[y]*ss2[y]^2);
a4[y_] := 6*cst*k*(-k^2 + 4*y^2)/(ss[y]*ss2[y]^3);
r2overr[y_] :=
1/(a0[y]^2*
a2[y]) (a4[y]*a0[y]^2 - 6*a3[y]*a1[y]*a0[y] - 3*a2[y]^2*a0[y] +
12*a2[y]*a1[y]^2);
V[y_] := r2overr[y];
numV[y_] := N[V[y] - 1, 30];
(*Wavenumber and initial conditions*)
Subscript[y, in] = -300;
expoi = -23;
expof = -16;
k = 10^(expof);
u0 = E^(-I Subscript[y, in])/Sqrt[2 k];
p0 = (- I E^(-I Subscript[y, in]))/Sqrt[2 k];
(* The system of ODEs*)
eqns = {x'[y] == p[y], p'[y] == numV[y]*x[y], x[0] == u0, p[0] == p0};
sol = NDSolve[eqns, {x, p}, {y, Subscript[y, in], 10^(20)*k},
WorkingPrecision -> 30, MaxSteps -> Infinity, MaxStepSize -> 0.01,
Method -> {"StiffnessSwitching", "NonstiffTest" -> False}]
(* Power spectrum *)
powB[y_] := (
k^5*(Re[Evaluate[x[y]]]^2 + Im[Evaluate[x[y]]]^2) /. sol[[1, 1]])/(
2*Pi^2*a2[y]^4*10^(350))
plotB = Plot[Log[powB[y] + 350], {y, Subscript[y, in], 10^(24)*k},
PlotStyle -> {Green},
AxesLabel -> {y, "\!\(\*SubscriptBox[\(P\), \(B\)]\)"}]
Can someone help me out and point me what I am doing wrong?
EDIT: I am editing this with the Matlab code I am trying to reproduce.
%{Definition of the ODE %}
function vel = velocity(y,xx)
global k b chi;
x=xx(1);
p=xx(2);
ss=sqrt(y^2+k^2);
ss2=(y^2+k^2);
a=b/chi*y^2/k^2+ss/k;
a1=y*(2*ss*b+chi*k)/ss/chi/k^2;
a2=(2*ss*b*ss2+chi*k^3)/ss/chi/k^2/ss2;
a3=-3*k*y/ss/ss2^2;
a4=3*k*(-k^4+3*k^2*y^2+4*y^4)/ss/ss2^4;
r2overr=(a4*a^2-6*a3*a1*a-3*a2^2*a+12*a2*a1^2)/a^2/a2;
vel(1,1)=p;
vel(2,1)=(r2overr-1)*x;
end
%{Program calling the previous function%}
global chi b k;
chi=1E25;
b=1370;
yin=-300;
expoi=-23;
expof=-16;
step=0.1;
ll=(expof-expoi)*10+1;
results=zeros(1,ll);
xx=zeros(1,ll);
id=1;
for expo=expoi:step:expof
k=10^(expo);
vin=exp (-1i*yin)/sqrt(2*k);
pin=-1i*exp (-1i*yin)/sqrt(2*k);
options1=odeset('RelTol',1e-10);
[T1,Y1]=ode45(@velocity,[-300 1E20*k],[vin pin],options1);
temp=Y1(size(Y1));
temp=temp (1,1)/1E175;
temp=real (temp).^2+imag (temp).^2
results(id)=log10(k^5*temp)+350;
xx(id)=expo;
id=id+1;
end
ys8=zeros(1,ll);
ys3=zeros(1,ll);
for id=1:ll
ys8(id)=-8*(xx(id)+23)+results(1);
ys3(id)=-3*(xx(id)+20.5)+results(26);
end
plot(xx,results,'Color','black');
hold on;
plot(xx,ys8,'Color','blue')
hold on;
plot(xx,ys3,'Color','red');




numV[y_] := N[V[y] - 1, 10];andWorkingPrecision -> 30– Alex Trounev Feb 02 '19 at 19:08