Savitzky–Golay method to find the first derivative

Question

I have a list of positions as a function of time data and want to apply the Savitzky–Golay method to find the first derivative. What is the approach I should take. I already know how to apply the filter.

Answer 1

This may be what you want. First I generate a sine wave with some noise.

data = Table[{t, Sin[2 π 123 t] + RandomReal[{-0.2, 0.2}]}, {t, 0,
    0.02, 0.0005}]; Dimensions@data

{41, 2}

Show[
 ListLinePlot[data, Mesh -> All],
 Plot[Sin[2 π 123 t], {t, 0, 0.02}, PlotStyle -> Purple]
 ]

Now we generate the kernel of a derivative filter for Savitzky Golay smoothing.

k = SavitzkyGolayMatrix[{5}, 3, 1];

Look this up in Help. We now apply this to the data using ListConvolve

c = ListConvolve[k, data[[All, 2]]];

Here I have lost 5 points from the start and end of the data due to the convolution process. Putting this back with the time base and plotting the analytical derivative of the sin curve (which is cos) we can see if the smoothed derivative has worked.

Show[
 ListLinePlot[Transpose[{data[[All, 1]][[6 ;; -6]], c}], Mesh -> All],
 Plot[-0.0005 2 π 123 Cos[2 π 123 t], {t, 0, 0.2}, 
  PlotStyle -> Purple]
 ]

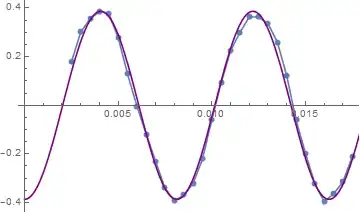
This is a reasonable calculation of the derivative. I had to put in the time increment because that is not included in the filter. I am not sure why I needed the negative sign. I will have to experiment more.

Hope that helps.