Dealing with stiffness in solving Mukhanov-Sasaki equation

Question

The code that I wrote is rather long, but I have included the whole code.

 α = 1;
 A = 0.130364;
 f = 0.129551;
 V0 = 2.1*10^-10;
 V[ϕ_] := 
 V0*(Tanh[ϕ/Sqrt[6 α]] + 
 A*Sin[Tanh[ϕ/Sqrt[6]]/f])^2;

 ϕin = 5.85;
 dϕin = -V'[ϕin]/V[ϕin];

 sol = NDSolve[{ϕ0''[y] + 3*ϕ0'[y] - 
 1/2*(ϕ0'[y])^3 + (3 - 1/2*(ϕ0'[y])^2)*V'[ϕ0[y]]/
  V[ϕ0[y]] == 0, ϕ0[0] == ϕin, ϕ0'[0] == 
dϕin}, ϕ0, {y, 0, 56.2}, MaxStepSize -> Infinity]

 ϕ[y_] := ϕ0[y] /. sol;
 dϕ[y_] := ϕ0'[y] /. sol
 ddϕ[y_] := ϕ0''[y] /. sol

 ϵ[y_] := 0.5*ϕ'[y]^2;
 η[y_] := ϵ[y] - 
 0.5/ϵ[y]*dϕ[y]*ddϕ[y];

 Hub[y_] := V[ϕ[y]]/(3 - ϵ[y]);
 a[y_] := 5837.67*Exp[y];



k=10^20
Nin = y /. FindRoot[k == 100*a[y]*Sqrt[Hub[y]], {y, 0, 56}];
Nf = y /. FindRoot[k == 100^-1*a[y]*Sqrt[Hub[y]], {y, 0, 56}];
eqns = {u''[y] + (1 - ϵ[y])*
  u'[y] + (k^2/(
    a[y]^2*Hub[
      y]) + (1 + ϵ[y] - η[y])*(η[y] - 
       2) - ϵ'[y] + η'[y])*u[y] == 0, 
v''[y] + (1 - ϵ[y])*
  v'[y] + (k^2/(
    a[y]^2*Hub[
      y]) + (1 + ϵ[y] - η[y])*(η[y] - 
       2) - ϵ'[y] + η'[y])*v[y] == 0, 
u[Nin] == 1/Sqrt[2*k], u'[Nin] == 0, v[Nin] == 0, 
v'[Nin] == -Sqrt[k]/(Sqrt[2]*k*10^-2)};
sol1 = NDSolve[eqns, {u, v}, {y, Nin, Nf}, MaxStepSize -> Infinity, 
Method -> {"StiffnessSwitching", 
Method -> {"ExplicitRungeKutta", Automatic}}];
uu[y_] := u[y] /. sol1;
vv[y_] := v[y] /. sol1;
Pspeck[y_] := 
k^3/(2*π^2)*(Abs[(uu[y] + I vv[y])/(a[y]*dϕ[y])])^2;
LogPlot[Pspeck[y], {y, Nin, Nf}]

So, I'm trying to solve the ODE for values of $k$ in the range $10^2$ to $10^{22}$. The initial point is computed when $k=100a(N)H(N)$ (I have used $y$ in the code). The purpose then is to solve this equation and compute the quantity $$P_{\zeta}(k)= \frac{k^3}{2\pi^2}\frac{|u_{k}+iv_{k}|^2}{z^2} $$ and extract the value of this expression when $k=100^{-1}a(N)H(N)$. The expectation is that the solution of $P_{\zeta}(k)$ will become constant more or less after $k=a(N)H(N)$. The code works perfectly upto around $k=10^{15}$ but, after that, I'm not getting the desired behaviour. 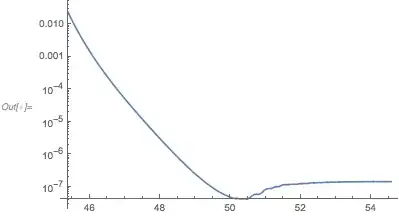For example, at $k=10^{20}$, the solution that I get is 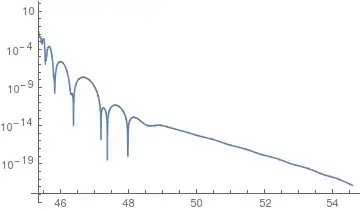as opposed to $10^{15}$, for which I get

Moreoever, the solution behaves rather erratically for large $k$ values. Using stiffness switching does not help. I am looking for a behaviour similar to that of $k=10^{15}$ where the solution becomes constant after $k=aH$. There is also convergence issues with the findroot method for large $k$ values. Any help would be appreciated.

Answer 1

Raising WorkingPrecision seems to help (it's good to Rationalize the inputs first):

k = 10^20;
Nin = y /. FindRoot[
    k == 100*a[y]*Sqrt[Hub[y]] // Rationalize[#, 0] & // Evaluate,
    {y, 0, 56}, WorkingPrecision -> 20];
Nf = y /. FindRoot[
    k == 100^-1*a[y]*Sqrt[Hub[y]] // Rationalize[#, 0] & // Evaluate,
    {y, 0, 56}, WorkingPrecision -> 20];
eqns = {u''[y] + (1 - ϵ[y])*
       u'[y] + (k^2/(a[y]^2*
            Hub[y]) + (1 + ϵ[y] - η[y])*(η[y] - 
            2) - ϵ'[y] + η'[y])*u[y] == 0, 
    v''[y] + (1 - ϵ[y])*
       v'[y] + (k^2/(a[y]^2*
            Hub[y]) + (1 + ϵ[y] - η[y])*(η[y] - 
            2) - ϵ'[y] + η'[y])*v[y] == 0, 
    u[Nin] == 1/Sqrt[2*k], u'[Nin] == 0, v[Nin] == 0, 
    v'[Nin] == -Sqrt[k]/(Sqrt[2]*k*10^-2)} // Rationalize[#, 0] &;
sol1 = NDSolve[eqns, {u, v}, {y, Nin, Nf}, MaxStepSize -> Infinity, 
   WorkingPrecision -> 20];
uu[y_] = u[y] /. sol1;
vv[y_] = v[y] /. sol1;
Pspeck[y_] := k^3/(2*π^2)*(Abs[(uu[y] + I vv[y])/(a[y]*dϕ[y])])^2;
LogPlot[Pspeck[y], {y, Nin, Nf}]

Answer 2

The underlying issue seems to be the same as mentioned in this post, because AccuracyGoal helps:

sol1 = NDSolve[eqns, {u, v}, {y, Nin, Nf}, AccuracyGoal -> 16];